Contenidos
Media aritmética
Promedio que se obtiene al sumar todos los datos y dividirlos por la cantidad total de datos.
Definición
La media aritmética, también conocida como promedio, es el valor que se obtiene al sumar todos los datos y dividirlos por la cantidad total de datos.
Uno de los problemas fundamentales que confronta un análisis estadístico consiste en buscar un valor representativo de una serie de valores; es decir que si se tiene una cantidad que varía, ya sea en el espacio o en el tiempo, se necesitará obtener su nivel predominante.
El valor que brinda este grado o nivel predominante es la media.
Cuando se calcula la media aritmética se desprecia la variación y tan solo interesa el valor predominante, lo cual es una gran ventaja en el resumen estadístico.
El valor de la media aritmética depende de cada una de las medidas que forman la serie y se halla afectado por las desviaciones extremas con respecto al promedio.
Usos
Los usos de la media aritmética son los siguientes:
- La media aritmética es el promedio más utilizado debido a que puede ser calculado para cualquier tipo de progresión, lógicamente con preferencia en las que siguen una progresión aritmética.
- Es aplicable en aquellas series donde, por existir términos iguales a cero o negativos, algunos promedios no pueden calcularse. Así también en series homogéneas o cuando existen grandes variaciones entre los términos que las forman.
- Se usa también el promedio aritmético en el caso de variaciones proporcionales.
Cálculo
El valor de la media aritmética se obtiene al sumar todos los datos que se tienen y dividir el resultado entre el número total de esos datos.
Publicidad, continua debajoLos promedios aritméticos se dividen en simple y ponderados:
- Simple: aquel que atribuye la misma importancia a los distintos términos de la serie o, expresado en términos técnicos, el mismo peso, la misma ponderación.
- Ponderado: aquel en que cada término de la serie de valores se encuentra influido por un factor cuantitativo que lo modifica totalmente; tal como se indicó, este factor cuantitativo se denomina peso o ponderación.
El símbolo del promedio aritmético es y la media aritmética simple se calcula de la siguiente manera:
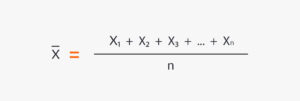
Dado lo anterior, el cálculo de la media aritmética para los valores 4, 6, 8, 10, 16, 28 sería el siguiente:
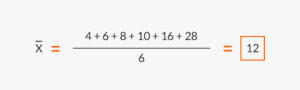
Respecto a la media aritmética ponderada, si se tiene una serie de valores X₁, X₂, X₃, …Xn, siendo sus respectivas ponderaciones P₁, P₂, P₃, … Pn, la media aritmética ponderada vendrá dada por la siguiente fórmula:
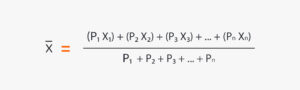
Con base a lo señalado y de acuerdo con los siguientes datos, si diferentes unidades de un determinado artículo se han vendido a precios distintos, tal como se muestra a continuación…
- 16 unidades a US$ 8.
- 20 unidades a US$ 5.
- 18 unidades a US$ 7.
…el cálculo del precio promedio ponderado del artículo vendido sería:

Ejemplos
Media aritmética simple
A continuación se muestran las edades de los 22 jugadores de la selección de balompié de Brasil, quienes participaron en el Campeonato Mundial de Fútbol de México 1970:
| Jugador | Edad |
|---|---|
| Felix | 32 |
| Ado | 25 |
| Leao | 20 |
| Brito | 30 |
| Wilson Piazza | 27 |
| Carlos Alberto | 25 |
| Marco Antonio | 19 |
| Baldochi | 24 |
| Fontana | 29 |
| Everaldo | 25 |
| Joel Camargo | 23 |
| Ze Maria | 21 |
| Clodoaldo | 20 |
| Gerson | 29 |
| Tostão | 23 |
| Rivelino | 24 |
| Paulo César | 21 |
| Jairzinho | 25 |
| Pelé | 29 |
| Roberto | 25 |
| Edu | 20 |
| Dario | 24 |
La sumatoria total de las edades es de 540. Para la determinación de las edades de cada uno de los integrantes de la selección campeona se tomaron los años cumplidos que tenían los jugadores al momento de la escenificación del Mundial México 70.
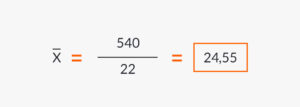
Con el promedio de edad de 24-55 años, la selección brasileña que deslumbró a los aficionados del fútbol en el Mundial de México 1970 ha sido, hasta ahora, el equipo más joven de la historia en lograr esta corona.
Media aritmética ponderada
En la empresa Ejemplo, C.A., la nómina de 100 obreros tiene la siguiente distribución salarial:
| Nro de obreros | Salario mensual en US$ |
|---|---|
| 40 | 800 |
| 25 | 1.000 |
| 20 | 1.250 |
| 15 | 1.500 |
La información anterior se ordenaría de la siguiente manera:
| X | Salarios | 800 | 1.000 | 1.250 | 1.500 | |
| P | Ponderación | 40 | 25 | 20 | 15 |
Y a efectos determinar la media aritmética ponderada, la información se completaría como sigue:
| X | 800 | 1.000 | 1.250 | 1.500 | Total |
| P | 40 | 25 | 20 | 15 | |
| X*P | 32.000 | 25.000 | 25.000 | 22.500 | 104.500 |
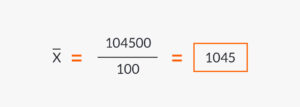
De acuerdo con esto, el resultado del promedio aritmético ponderado sería:
| Bibliografía: |
|---|
|
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana
 y la media aritmética simple se calcula de la siguiente manera:
y la media aritmética simple se calcula de la siguiente manera: