Contenidos
Moda estadística
Valor que se repite el mayor número de veces en un conjunto de datos.
Definición
La moda estadística es aquel valor que, dentro de un conjunto de datos, se repite el mayor número de veces.
La determinación de la moda estadística en un conjunto de datos que no están agrupados no requiere ningún tipo de cálculo, sino tan solo el conteo de las variables. Otra forma de determinar la moda en datos no agrupados consiste en verificar cuál es el valor de mayor frecuencia en una tabla de frecuencias absolutas.
La moda estadística es aplicable tanto para datos de información cualitativa como cuantitativa.
Tipos
La moda estadística se clasifica de la siguiente manera:
- Moda unimodal: tipo de moda estadística en la cual un único valor se repite el mayor número de veces dentro de un conjunto de datos.
- Moda bimodal: tipo de moda estadística en la que 2 valores diferentes presentan el mismo número máximo de repeticiones, dentro de un conjunto de datos.
- Moda multimodal: tipo de moda estadística en la que 3 o más valores diferentes presentan el mismo número máximo de repeticiones dentro de un conjunto de datos.
Moda estadística en datos agrupados
Cuando los datos de un conjunto se encuentran agrupados en intervalos, la moda estadística corresponde al punto medio del intervalo que presenta la mayor frecuencia.
Teniendo en cuenta lo anterior, el primer paso para calcular la moda en datos agrupados consiste en determinar cuál es el intervalo de mayor frecuencia en la tabla que contiene la información agrupada.
Posteriormente se realiza el cálculo de la moda aplicando la siguiente fórmula:
Publicidad, continua debajo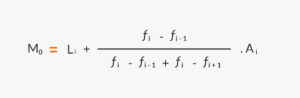
Fórmula para calcular la moda estadística.
Las variables que involucran la ecuación anterior son:
- Li: límite inferior del intervalo donde está ubicada la moda.
- fi-1: frecuencia absoluta del intervalo anterior donde está ubicada la moda.
- fi: frecuencia absoluta del intervalo donde está ubicada la moda.
- fi+1: frecuencia absoluta del intervalo siguiente donde está ubicada la moda.
- Ai: amplitud del intervalo donde está la moda.
Ejemplos
Algunos ejemplos de moda estadística son los desarrollados a continuación, utilizando el caso de una consultora que decide realizar una investigación en una oficina.
Ejemplo moda unimodal
Número de hijos que poseen los empleados. Luego de realizar la pregunta a 20 empleados, el conjunto de datos es el siguiente: [ 0, 2, 2, 0, 3, 5, 1, 2, 3, 1, 0, 2, 6, 4, 3, 4, 2, 0, 1, 2].
La moda del conjunto es 2, ya que este valor se repite 6 veces, mientras que el resto de los valores se repite un número de veces inferior.
Ejemplo moda bimodal
Edad de los empleados. Luego de realizar la pregunta a 20 empleados, el conjunto de datos es el siguiente: [25, 27, 25, 30, 28, 25, 30, 25, 32, 42, 51, 25, 27,30, 33, 30, 42, 40, 51, 30].
Así, la moda del conjunto es 25 y 30, ya que ambos se repiten 5 veces mientras que el resto de los valores se repite un número de veces inferior.
Ejemplo moda multimodal
Número de habitaciones que poseen sus viviendas. Luego de realizar la pregunta a 20 empleados, el conjunto de datos es el siguiente: [2, 3, 2, 2, 4, 1, 3, 3, 2, 3, 6, 5, 4,4, 2, 1, 1, 4, 4, 3].
La moda del conjunto es 2, 3 y 4, ya que estos valores se repiten 5 veces, mientras que el resto se repite un número de veces inferior.
Ejemplo moda en datos agrupados
Cuánto es el peso en kilos de los empleados. Luego de realizar la pregunta a 20 empleados, el conjunto de datos es el siguiente:
| Kilogramos | Frecuencia absoluta (Fa) |
| [50 – 60] | 1 |
| [60 – 70] | 4 |
| [70 – 80] | 2 |
| [80 – 90] | 8 |
| [90 – 100] | 5 |
| Sumatoria ∑ | 20 |
Para este cálculo de la moda estadística aplicamos los siguientes pasos:
- Se ubica el intervalo donde se encuentra la mayor frecuencia absoluta, en este caso en el intervalo [80 – 90] con frecuencia 8.
- Se aplica la fórmula para calcular la moda en datos agrupados:
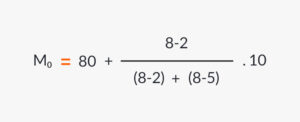
Obtenemos así que la moda estadística es de 87.
| Bibliografía: |
|---|
|
Contadora pública (CECAR - Corporación Universitaria del Caribe). Especialista en gestión pública (UNAD Colombia). Diplomado en normas contables (Universidad de Colombia). Escritora y redactora con 20 años de experiencia en lectura crítica.
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana