Contenidos

Inicio / Matemática / Álgebra / Progresión geométrica

Progresión geométrica

Secuencia de números reales en la que cada término posterior se obtiene multiplicando el término anterior por una constante fija.

Por

Haude Medina

Tabla de contenidos:

Definición

Una progresión geométrica es una secuencia de números reales en la que cada término posterior se obtiene multiplicando el término anterior por una constante fija.

Esta constante se denomina razón de la progresión.

La progresión o sucesión geométrica se denota como (PG), donde, la relación entre cualquier término ${(a}_n)$ y su término anterior ${(a}_{n-1})$ es igual a la razón común (r).

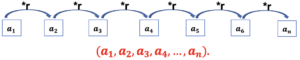
De esta manera, si se desea obtener el siguiente término de una sucesión geométrica se debe multiplicar el término actual por la constante.

En cambio, si se desea hallar el término anterior de la progresión, se divide el término con la misma razón común. Por claridad o simplicidad, se suele multiplicar por la inversa de la razón $\left(\frac{1}{r}\right)$ .

Elementos

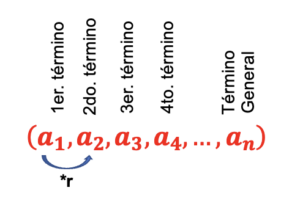
Para comprender mejor cómo funciona una progresión geométrica, es importante conocer sus elementos fundamentales:

Publicidad, continua debajo

Primer término: es el valor inicial de la secuencia, se denota como ${(a}_1)$ y es el punto de partida desde el cual se generan los términos sucesivos.
Razón: es la constante que se utiliza para obtener cada término posterior multiplicando el término anterior. Se representa como $r$ y determina el crecimiento o decrecimiento de la secuencia y debe ser diferente de cero.
Término general: se utiliza para representar cualquier término de la secuencia en función de su posición ${(a}_n)$ .
Término específico: se refiere a un término particular de la progresión geométrica, identificado por su posición ${(a}_k)$ en la secuencia. Por ejemplo, ${(a}_5)$ es el quinto término de la sucesión.
Número de términos $(n)$ : es la cantidad de números que componen la progresión.

elementos de las progresiones geométricas

Razón

El método más sencillo para hallar la razón de una progresión geométrica es dividiendo dos términos consecutivos:

La fórmula para calcular la razón (r) de la sucesión geométrica es la siguiente:

$r=\frac{a_n}{a_{n-1}}$

Donde:

${(a}_n)$ es el término enésimo de la progresión.
${(a}_{n-1})$ es el término anterior al enésimo término.

Término general

La fórmula del término general de una progresión geométrica permite calcular cualquier término de la secuencia a partir de su posición, sin necesidad de conocer todos los anteriores.

Esta expresión se basa en la relación multiplicativa entre los términos consecutivos de la progresión. Se representa como:

$a_n=a_1\ast r^{n-1}$

Donde:

$a_n$ : es el término general que se desea calcular, correspondiente a la posición (n) en la secuencia.
$a_1$ : es el primer término de la progresión.
$r$ : es la razón común de la progresión.
$n$ : es la posición del término en la secuencia.

Para comprender mejor cómo utilizar esta fórmula, veamos el siguiente ejemplo:

Se tiene la progresión geométrica con $a_1=2$ (primer término) y $r=3$ (razón común).

Se quiere encontrar el quinto término de la secuencia ${(a}_5)$ .

Se aplica la fórmula del término general y se sustituyen los valores conocidos:

$a_n=a_1\ast r^{n-1}$

$a_1=2$ .
$r=3$ .
$n=5$ .

$a_5=2\ast\left(3\right)^{5-1}=2\ast\left(3\right)^4=2\ast81$

$a_5=162$

Por lo tanto, el quinto término de la progresión geométrica es 162.

Primer término

En una progresión geométrica cuando se desconoce su primer término, este se puede hallar a partir de la fórmula del término general de la manera siguiente:

Se conoce que la expresión del término general es:

$a_n=a_1\ast r^{n-1}$

Despejando ${(a}_1)$ que es el primer término se obtiene:

$a_1=\frac{a_n}{r^{n-1}}$

Suma de términos

La suma de los primeros (n) términos de una progresión geométrica es una cantidad importante que permite calcular la suma total de una serie de valores que siguen un patrón multiplicativo.

Esta suma de se refiere a todos los términos que van desde ${(a}_1)$ hasta $(a_n)$ , incluyendo ambos.

Para encontrar esta suma se pueden utilizar las siguientes fórmulas:

Esto si r ≠ 1.

Ejemplos

Veamos algunos ejemplos de sucesiones geométrica que permitirán comprender mejor lo explicado anteriormente.

Ejemplo #1

3, 12, 48, 192, 768, 3072, …

El primer término: $a_1=3$ . Si se divide el término siguiente entre el primer término se puede conocer la razón.

$r=\frac{a_n}{a_{n-1}}=\frac{12}{3}$

$r=4$

Se puede comprobar que cada término, menos el primero, se obtiene multiplicando el anterior por 4:

$a_1\ast{r=a}_2\ \Rightarrow 3\ast4=12$
$a_2\ast{r=a}_3\ \Rightarrow 12\ast4=48$
$a_3\ast{r=a}_4\ \Rightarrow 48\ast4=192$ Así sucesivamente

Ejemplo #2

84, 42, 21, 10.5, 5.25, …

Para esta PG el primer término $a_1=84$ y la razón es $r=\frac{1}{2}$ que resulta de al dividir:

$r=\frac{a_n}{a_{n-1}}=\frac{42}{84}=0.5=\frac{1}{2}$

Para verificar que esto es cierto se multiplica cada término por $\frac{1}{2}$ .

$a_1\ast{r=a}_2\ \Rightarrow 84\ast\frac{1}{2}=42$
$a_2\ast{r=a}_3\ \Rightarrow 42\ast\frac{1}{2}=21$
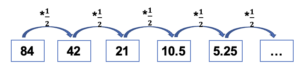
$a_3\ast{r=a}_4\ \Rightarrow 21\ast\frac{1}{2}=10.5$ . Así sucesivamente.

En ambos ejemplos, la razón es constante, que es la característica principal de una progresión geométrica.

Ejercicios resueltos

Ejercicio #1

Se conoce el tercer y cuarto término de una progresión geométrica y se debe hallar la razón común para $a_3=18$ y $a_4=54$ .

Ver solución

Se conoce que la razón de una progresión geométrica se halla dividiendo dos términos consecutivos aplicando la expresión: $r=\frac{a_n}{a_{n-1}}$ . Sustituyendo los términos se obtiene:

$r=\frac{54}{18}=3$

La razón de la progresión geométrica es igual a 3.

Ejercicio #2

Se tiene el siguiente término de una sucesión geométrica $a_5=-729$ y $r=-3$ . Hallar el primer término de la progresión.

Ver solución

Se utiliza la fórmula

$a_1=\frac{a_n}{r^{n-1}}=\frac{-729}{\left(-3\right)^{5-1}}=\frac{-729}{\left(-3\right)^4}=\frac{-729}{81}=-9$

$a_1=-9$

El primer término de la progresión geométrica es igual a -9.

PG: (-9, 27, -81, 243, -729, …)

Ejercicio #3

Se tiene una progresión geométrica con $a_1=2$ y $r=4$ . Calcular la suma de los primeros 6 términos de la secuencia $(S_6)$ .

Ver solución

Se tiene que $a_1=2, r=4, n=6$ . Aplicando la fórmula:

$S_n=a_1\ast\frac{r^n-1}{r-1}\rightarrow S_6=a_1\ast\frac{r^6-1}{r-1}$

$S_6=2\ast\frac{\left(4\right)^6-1}{4-1}=2\ast\frac{4096-1}{4-1}=2\ast\frac{4095}{3}$

$S_6=2 \ast 1365 = 2730$

La suma de los seis primeros términos es: $S_6=2730$ .

Bibliografía:
Moya, P. (2014). Matemáticas orientadas a las enseñanzas académicas. 3o B de ESO. Madrid: Libros Marea Verde. Stewart, J. 2006. Cálculo de una Variable. 7ma. Edición. Cengage Learning.

¿Te resultó útil este artículo?

¡Gracias!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2024). Progresión geométrica. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/progresion-geometrica/). Última edición: abril 2024. Consultado el 10 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!