Contenidos

Inicio / Matemática / Álgebra / Clasificación de los números

Matemática

Álgebra

Clasificación de los números

Agrupación de los números en diferentes conjuntos o categorías según sus propiedades y características particulares.

Por

Haude Medina

11m

Tabla de contenidos:

Definición

La clasificación de los números consiste en agrupar los números en diferentes conjuntos o categorías según sus propiedades y características particulares.

Esta categorización es importante en matemáticas por diferentes razones:

Organización lógica de los números: permite organizar los números de manera lógica, facilitando su comprensión y análisis.
Facilita la comprender como se relacionan: proporciona una base sólida para comprender cómo se relacionan entre sí, identificar patrones y conexiones en diferentes conjuntos de números.
Aplicaciones prácticas en diversos contextos: al comprender los diferentes conjuntos de números y sus propiedades, se adquieren las herramientas necesarias para abordar problemas más complejos y resolver una variedad de problemas en diferentes disciplinas matemáticas
Desarrollo de habilidades matemáticas avanzadas: permite desarrollar habilidades matemáticas para abordar problemas de manera precisa y sistemática en una variedad de contextos prácticos.

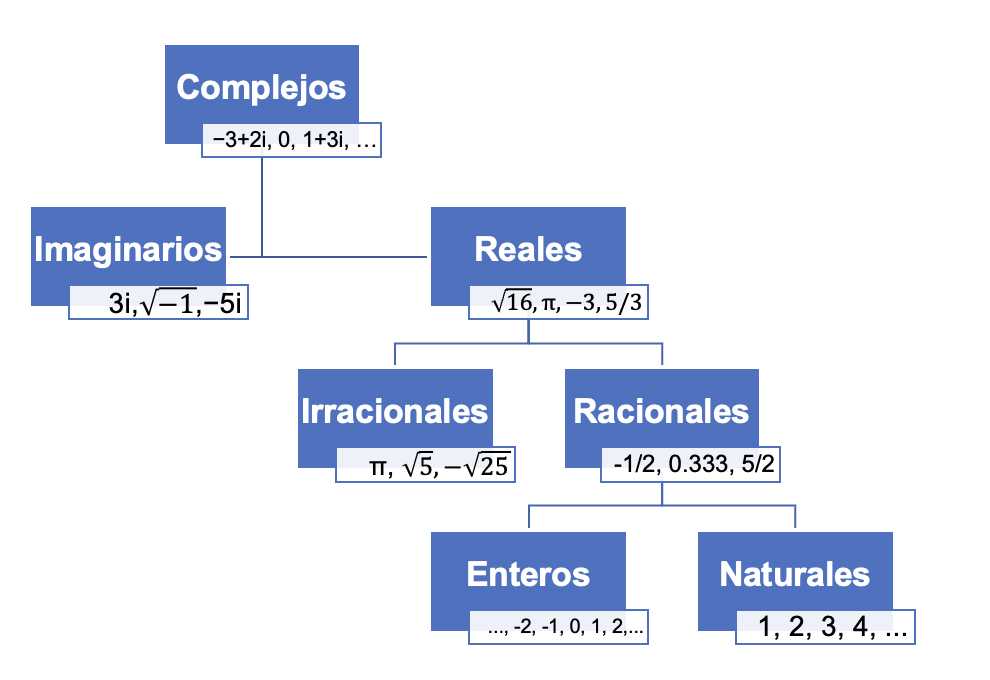
Gráfico de clasificación de los números.

Esta agrupación se realiza en 7 conjuntos principales que incluye los números naturales, enteros, racionales, irracionales, reales, los números complejos e imaginarios.

Como se observa en el gráfico de clasificación, muchos números están incluidos en varios conjuntos.

Cada conjunto de número se describe a continuación, con sus propiedades, tipos y ejemplos para su mejor entendimiento.

Números naturales

Artículo principal: Números naturales.

Los números naturales son aquellos utilizados para contar elementos o representar cantidades enteras no negativas, como 1, 2, 3, 4, y así sucesivamente.

Este conjunto de números está representado en la recta numérica desde el 1 hasta el infinito (∞), ubicándose del lado derecho del cero (0) sin incluirlo y se denotan con la letra $\mathbb{N}$ , tal que:

Publicidad, continua debajo

$\mathbb{N}=\left\{1,2,3,4,5,6,7,\ldots\infty\right\},\ \ \mathbb{N}\setminus\left\{0\right\}$

Características

El conjunto de los números naturales, a pesar de ser el más elemental de los conjuntos de números, tiene características importantes definidas y que se utilizan para el resto de conjuntos numéricos.

Es un conjunto ordenado donde cada número tiene una posición única en la recta numérica, por lo que se puede establecer relaciones de orden como mayor que (>), menor que (<) e igual que (=).
Es un conjunto infinito, ya que siempre hay otro número natural mayor que cualquier número natural dado.
Cada número natural tiene un sucesor único, que otro número natural, que le sigue en la recta numérica.
Los números naturales representan cantidades discretas, sin partes fraccionarias o decimales.
Tradicionalmente, el número cero no se incluye en los números naturales. Sin embargo, en algunos contextos puede considerarse como parte de estos.

Números enteros

Artículo principal: Números enteros.

El conjunto de los números enteros se denota con la letra $\mathbb{Z}$ e incluyen tanto los números naturales como sus negativos y el cero.

Se utilizan para representar cantidades completas, ya sea positivas, negativas o neutras.

Se representan en la recta numérica tanto a la derecha como a la izquierda del cero: …, -3, -2, -1, 0, 1, 2, 3, …

Propiedades

Propiedad Interna: tanto la suma como la multiplicación de números enteros siempre dan como resultado otro número entero. Ejemplo: (-5) + 4 = -1, donde (-1) es un número entero. 6 * 3 = 18, donde 18 es un número entero.
Propiedad Conmutativa: el orden de los sumandos en una suma o de los factores en una multiplicación no afecta el resultado. Ejemplo: Suma: 100 + (-53) = (-53) + 100 = 47. Multiplicación: (-8) * 3 = 3 * (-8) = -24.
Propiedad asociativa: la forma en que se agrupan los números enteros en la suma o multiplicación no afecta el resultado. Ejemplo: Suma: (30 + 5) – 20 = 30 + (5 – 20).
Elemento neutro de la suma: el elemento neutro es el cero (0). Sumar cualquier número entero con cero da como resultado el mismo número entero. Ejemplo: 55 + 0 = 55.
Elemento neutro de la multiplicación: el elemento neutro es el uno (1). Multiplicar cualquier número entero por uno da como resultado el mismo número entero. 23 * 1 = 23.
Elemento opuesto: sumar cualquier número entero con su opuesto da como resultado cero (0). Ejemplo: 25 + (-25) = 0

Números racionales

Artículo racionales: Números racionales.

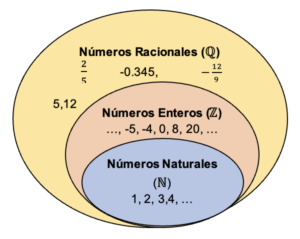
Se define un número racional, como aquel número que puede expresarse en forma de fracción.

Estos son de la forma $\frac{a}{b}$ , donde el numerador “a” y el denominador “b” son números enteros ( $\mathbb{Z}$ ), y b > 0.

El conjunto de los números racionales se denota con la letra $\mathbb{Q}\$ y, dentro de este conjunto están los números naturales ( $\mathbb{N}$ ) y enteros ( $\mathbb{Z})$ . Donde, $\mathbb{N}\in \mathbb{Z}\in\mathbb{Q}\$ .

La relación de pertenencia se muestra en la figura a continuación:

Propiedades

Son cerrados bajo operaciones de suma, resta, multiplicación y división. Esto significa que siempre da como resultado otro número racional.
Pueden tener una representación decimal finita o infinita periódica. Ejemplo: $\frac{1\ }{2}=0.5$ (finito), $\frac{1}{3}\ =\ 0.333$ (infinito periódico) , $\frac{5}{6}\ =\ 0.833$ (infinito periódico).
Pueden ser positivos o negativos.
La propiedad conmutativa establece que el orden de los números en una operación no afecta el resultado. Para la suma: $\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}$ . Multiplicación $\frac{a}{b}\ast\frac{c}{d}=\frac{c}{d}\ast\frac{a}{b}$ .
La propiedad asociativa establece que la forma en que se agrupan los números en una operación no afecta el resultado. En la suma: $\frac{a}{b}+\left(\frac{c}{d}+\frac{g}{h}\right)=\left(\frac{a}{b}+\frac{c}{d}\right)+\frac{g}{h}$ . Para la multiplicación: $\frac{a}{b}\ast\left(\frac{c}{d}\ast\frac{g}{h}\right)=\left(\frac{a}{b}\ast\frac{c}{d}\right)\ast\frac{g}{h}$ .
El elemento neutro es aquel que, al ser operado con otro número, no altera su valor. Para la suma, $\frac{a}{b}+0=\frac{a}{b}$ . Para la multiplicación, $\frac{a}{b}\ast1=\frac{a}{b}$ .
La propiedad distributiva establece cómo se relacionan la suma y resta con la multiplicación. Se expresa como $\frac{a}{b}\ast\left(\frac{c}{d}\pm\frac{g}{h}\right)=\left(\frac{a}{b}\ast\frac{c}{d}\right)\pm\left(\frac{a}{b}\ast\frac{g}{h}\right)$ .

Números irracionales

Artículo principal: Números irracionales.

Son números que no pueden expresarse como una fracción y tienen una expansión decimal infinita no periódica. Ejemplos comunes son $\sqrt2$ y el número pi (π).

Los números Irracionales se denota con la letra $\mathbb{I}$ y son un subconjunto de los números Reales $\left(\mathbb{R}\right)$ , pero que no pertenecen a los números Racionales ( $\mathbb{Q}$ ).

$\mathbb{I}=\mathbb{R}\setminus\mathbb{Q}\ \ \ \left\{x\in\mathbb{R}\middle| x\notin\mathbb{Q}\right\}$

Propiedades

- La división entre 0 no está definida entre los números irracionales.
- La suma y la multiplicación entre números irracionales no siempre es otro número irracional.
- La suma o resta de un número racional más un número irracional, da como resultado un irracional. Sea, $a\in\mathbb{Q},\ \ b\ \in\mathbb{I}\ \Rightarrow a\pm b\ \in\mathbb{I}$ .
- La multiplicación de un número racional diferente de cero, por un irracional da como resultado un número irracional. $a\in\mathbb{Q},\ \ b\ \in\mathbb{I}\ \Rightarrow a\ast b\ \in\mathbb{I}$ .
- La división entre un número racional diferente de cero y un número irracional, el cociente es un número irracional. $a\in\mathbb{Q},\ \ b\ \in\mathbb{I}\ \Rightarrow\frac{a}{b}\ \in\mathbb{I}$ .
- El inverso de un número irracional (elevado -1) es otro número irracional. $a\in\mathbb{I}\Rightarrow a^{-1}\ \in\mathbb{I}$ .

Para la suma y la multiplicación de números irracionales se cumple la propiedad conmutativa. a + b = b + a , donde $\ a,b\in\mathbb{I}\$ y para la multiplicación $a\ast b=b\ast a$ , donde $\ a,b\in\mathbb{I}$ .
Para la adición y el producto de irracionales se verifica la propiedad asociativa. $\left(a+b\right)+c=a+\left(b+c\right)$ , $\ donde\ a,b,c\in\mathbb{I}\$ y para la multiplicación $\left(a\ast b\right)\ast c=a\ast(b\ast c),$ donde $\ a,b,c\in\mathbb{I}$ .

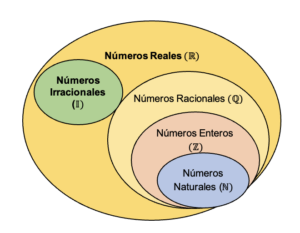
Números reales

Artículo principal: Números reales.

Los números reales constituyen el conjunto más amplio de número incluyen tanto a los números racionales como a los irracionales.

También se puede decir, que cualquier número racional o irracional es un número real, $\mathbb{R}\ =\ \mathbb{Q}\ (\ \mathbb{I}$ .

Propiedades

Entre cualquier par de números reales existe otro número real. Esto significa que están densamente distribuidos en la recta numérica.
Son un conjunto cerrado bajo las operaciones básicas, es decir; cualquier operación de dos números reales siempre da como resultado otro número real.
Las propiedades conmutativa y asociativa se cumplen para la suma y multiplicación de números reales:
- Suma: conmutativa: $a\ +\ b\ =\ b\ +\ a$ . Asociativa: $(a\ +\ b)\ +\ c\ =\ a\ +\ (b\ +\ c)$ .
- Multiplicación: conmutativa: a\ \ast\ b\ =\ b\ \ast\ a. Asociativa: $(a * b) * c = a * (b * c)$ .
La multiplicación se distribuye sobre la suma en los números reales, lo que significa que: $a(b\ \pm\ c)\ =\ (a\ \ast\ b)\ \ \pm\ (a\ \ast\ c)$ .

Números imaginarios

Artículo principal: Números imaginarios.

Se define matemáticamente un número imaginario, como el resultado de la raíz cuadrada de un número negativo.

Los números imaginarios se construyen a partir de su base, que es la “unidad imaginaria” y se denota con la letra “i”.

Provienen de dar solución a la expresión $\sqrt{-1}$ .

$i=\sqrt{-1},\ por\ lo\ tanto\ i^2=-1\$

Propiedades

Hay una propiedad interesante de “i”, cuando se eleva a diferentes potencias, este pasa por cuatro valores diferentes completando un ciclo.

$i^0=1$
$i^1=i$
$i^2=-1$
$i^3=-i$
$i^4=1$
$i^5=i$
$i^6=-1$
$i^7=-i$

Se puede observar, que los resultados exponenciales de “i” se repiten cada cuatro valores siendo, 1, i, -1, -i.

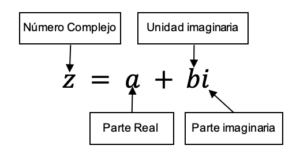
Números complejos

Artículo principal: Números complejos.

El conjunto de los números complejos se forma de la combinación de un número real y un número imaginario y se denotan con la letra $\mathbb{C}$ . En términos de conjuntos:

$\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$

Se puede definir este conjunto de números, como aquellos que se escriben en la forma a + bi.

Propiedad de cierre o cerradura: para la suma: $z_1, z_2 \in\mathbb{C}$ , se tiene que $\ z_1+\ z_2\ \in\mathbb{C}$ . En la multiplicación $z_1, z_2\ \in\mathbb{C}$ , se tiene que $\ z_1\ast\ z_2\ \in\mathbb{C}$ .
Propiedad conmutativa: en la suma: $z_1, \ z_2\ \in\mathbb{C}$ , se cumple que $\ z_1+\ z_2=\ z_2+z_1$ . En el caso de la multiplicación: $z_1, z_2\ \in\mathbb{C}$ , se cumple que $z_1\ast\ z_2=\ z_2\ast z_1$ .
Propiedad asociativa: en la suma esta propiedad se expresa como: $z_1, \ z_2,\ z_3\ \in\mathbb{C}$ , se cumple que $\ {(z}_1+\ z_2)+z_3\ =\ z_1+{(z}_2+z_3)$ . En el caso de la multiplicación $z_1,\ z_2,\ z_3\ \in\mathbb{C}$ , se cumple que ${(z}_1\ast\ z_2)\ast z_3\ =\ z_1\ast{(z}_2\ast z_3)$ .
Propiedad distributiva: $z_1,\ z_2,\ z_3\ \in\mathbb{C}$ , se cumple que $z_1\ast{(z}_2\pm z_3)=z_1\ast z_2\pm z_1\ast z_3$ .

Bibliografía:
Benavent, R. C. (abril 2016). Números reales y números complejos (Spanish Edition). Bubok Publishing. Francesca Pensieri, A. A. (1979). Números Complejos (2a ED.). Reverte. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador. Ministerio de Educación del Ecuador. (2016). Matemática 9° grado. Libro del estudiante. SMEcuaediciones. Ministerio de Educación del Ecuador. (2016b). Matemática 10° grado. Libro del estudiante. SMEcuaediciones.

Bibliografía:

Benavent, R. C. (abril 2016). Números reales y números complejos (Spanish Edition). Bubok Publishing.
Francesca Pensieri, A. A. (1979). Números Complejos (2a ED.). Reverte.
Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador.
Ministerio de Educación del Ecuador. (2016). Matemática 9° grado. Libro del estudiante. SMEcuaediciones.
Ministerio de Educación del Ecuador. (2016b). Matemática 10° grado. Libro del estudiante. SMEcuaediciones.

¿Te resultó útil este artículo?

¡Gracias!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2024). Clasificación de los números. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/clasificacion-de-los-numeros/). Última edición: abril 2024. Consultado el 10 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!