Teorema de Rolle

Definición

El Teorema de Rolle es una herramienta importante en el cálculo diferencial que permite encontrar puntos críticos de una función diferencial en intervalos cerrados a partir de la información sobre su comportamiento en los extremos de un intervalo.

En términos simples, el Teorema de Rolle establece lo siguiente:

Si una función es continua en un intervalo cerrado y además derivable en ese intervalo, y que se cumpla que su valor en los extremos del intervalo es el mismo, entonces, en algún punto dentro del intervalo la pendiente (o derivada) de la función será igual a cero.

Expresado de forma matemática, el Teorema de Rolle debe cumplir 3 axiomas:

Si una función  cumple las siguientes condiciones:

• Es continua en el intervalo cerrado [a,b].
• Es derivable en el intervalo abierto (a,b).
• Sus valores en los extremos del intervalo son iguales, es decir, .

Entonces, el teorema permite afirmar que:

existe al menos un punto c dentro del intervalo (a,b) tal que la derivada de la función en ese punto es igual a cero, es decir, .

Como c, se encuentra entre a y b, entonces, (a < c < b).

El Teorema de Rolle, fue enunciado por el matemático francés Michel Rolle en 1691 y es un caso especial del «Teorema del Valor Medio de Lagrange».

Análisis de los enunciados

• Continuidad en el intervalo cerrado [a, b]: la función no debe tener «saltos» o discontinuidades dentro del intervalo, por lo que, la gráfica de la función debe ser una curva continua sin interrupciones.
• Derivabilidad en el intervalo abierto (a, b): la función debe tener una derivada definida en todos los puntos del intervalo, excepto en los extremos. La derivada indica la pendiente de la recta tangente a la gráfica de la función en cada punto.
• Igualdad de los valores en los extremos: la función debe tomar el mismo valor en ambos extremos del intervalo. La gráfica de la función «toca» el mismo punto en  x = a y en  x = b.
• Existencia de un punto con derivada nula: si se cumplen las tres condiciones anteriores, entonces existe un punto dentro del intervalo donde la derivada de la función es cero.

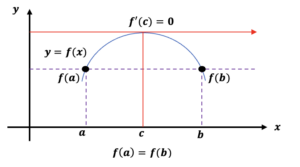
Interpretación gráfica

En la gráfica, se observar que la curva de la función y = f(x) es continua en el intervalo [a, b], es decir; entre x = a y x = b , y para cada punto dentro del intervalo.

Además, es derivable en (a, b) y los puntos a y b tienen la misma altura, por lo que f(a) = f(b).

Siendo posible trazar una tangente a la curva, donde existe un punto c que se encuentra dentro del intervalo (a, b), lo que significa que f‘(c) = 0.

Por el contrario, si en un intervalo (a, b) no existe un valor c que anule la derivada, se debe a que alguna de las premisas no se cumple.

Procedimiento

El teorema de rolle no tiene una fórmula específica de resolución, ya que son premisas que deben cumplirse.

Mediante un ejemplo práctico, se explicarán los pasos a realizar para encontrar el punto  y determinar si se cumple el teorema.

Ejemplo práctico: verificar el teorema de rolle para la función: en el intervalo [1,3].

Verificación de las condiciones:

Paso 1:

f(x) es continua en [1,3]: Por ser una función polinómica es continua en todo su dominio de definición.

Paso 2:

f(x) es diferenciable en (1,3): De igual manera, por ser una función polinómica es derivable.

Paso 3:

Verificar si f(a)=f(b) en el intervalo dado: Para esto se introducen los valores de a y b en la función.

Se cumple que f(a) = f(b), ya que, f(1) = 0 y f(3) = 0.

Por cumplirse las 3 condiciones del teorema de rolle, tan solo falta comprobar que:

Paso 4:

Para encontrar el punto c se halla la primera derivada de y se iguala a 0, para comprobar su comportamiento.

Se iguala la derivada f'(c) = 0 para hallar el punto c en el intervalo (1,3)

Interpretación de resultados:

El Teorema de Rolle dice que existe al menos un punto c en (1,3) donde f'(c). En este caso, c= 2 y anula la derivada para f'(2) = 0, confirmando la aplicación del teorema.

De tal manera que la recta tangente en ese punto es paralela al eje x.

Ejercicio resuelto

Para la función , demostrar que satisface las condiciones del teorema de Rolle en el intervalo [-2,5] y encontrar los valores de c en (-2, 5) que satisfacen f'(c) = 0.