Contenidos
Puntos de inflexión
Puntos críticos en la gráfica de una función donde cambia la concavidad de la curva.
Definición
Los puntos de inflexión son puntos críticos en la gráfica de una función donde cambia la concavidad de la curva.
En otras palabras, son aquellos puntos donde la curvatura de la función cambia de cóncava hacia arriba a cóncava hacia abajo, o viceversa.
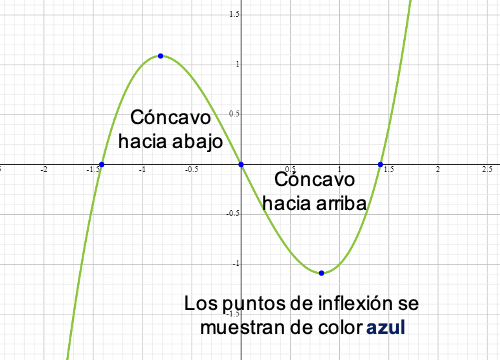
El punto de inflexión está representado por un par de coordenadas del plano cartesiano (x, y).
«Un punto de inflexión es un punto de la gráfica en el que la segunda derivada es igual a cero o indefinida y cambia de signo»
- Si
cóncava hacia arriba
- Si
cóncava hacia abajo
Análisis gráfico
Para entender mejor este concepto, consideremos una función y su gráfica.
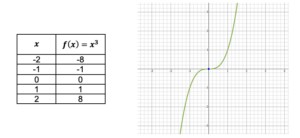
La función tiene un punto de inflexión en x = 0 porque la curva cambia de cóncava hacia arriba a cóncava hacia abajo en ese punto, como se observa en la gráfica de la función punto de inflexión (x, y) = (0, 0).
Utilidad
Los puntos de inflexión son importantes en el estudio de las funciones ya que nos proporcionan información sobre:
- Caracterización de la curva: estos puntos permiten comprender mejor cómo se comporta la función en diferentes intervalos y cómo cambia su concavidad.
- Análisis de cambios de dirección: los cambios de curvatura de la función pueden ser relevantes en diversos contextos, como en la economía, física o biología.
- Interpretación gráfica: al analizar gráficamente una función y sus los puntos de inflexión ayudan a comprender la «suavidad» de la curva y a identificar regiones donde la función cambia su comportamiento de manera significativa.
- Aplicaciones prácticas: en campos como la ingeniería, la economía, la física y la biología, el estudio de los puntos de inflexión es esencial para comprender fenómenos naturales o modelar sistemas complejos.
Características
- Cambio de concavidad: la característica principal de un punto de inflexión es que marca un cambio en la concavidad de la curva de la función. Esto diferencia los puntos de inflexión de otros puntos en la gráfica de una función.
- Anulación de la segunda derivada: el cambio en la concavidad de la función en un punto , es un punto de inflexión si la segunda derivada de la función se anula en
- No necesariamente extremos locales: a diferencia de los máximos y mínimos locales, los puntos de inflexión no necesariamente representan extremos de la función, ya que pueden estar ubicados en cualquier parte de la gráfica donde cambia su concavidad.
- Intersección de la tangente: en un punto de inflexión, la tangente a la curva de la función puede cruzar la curva misma. Esto se debe al cambio de concavidad en el punto, lo que hace que la tangente pase de estar por encima de la curva a estar por debajo de ella, o viceversa.
- Puntos de referencia: los puntos de inflexión sirven como puntos de referencia importantes al analizar gráficamente una función. Ayudan a comprender la forma de la curva y proporcionan información sobre cómo se comporta la función en diferentes intervalos.
Métodos de identificación
Existen varios métodos para identificar los puntos de inflexión de una función.
Cambio de signo de la primera derivada
- La primera derivada de una función se relaciona con la pendiente.
- Calcular la primera derivada de la función f(x).
- Criterio: un punto de inflexión ocurre cuando la primera derivada cambia de creciente a decreciente o viceversa (cambia el signo de la primera derivada). Si la primera derivada es positiva, la función es creciente y cóncava hacia arriba. Si es negativa, la función es decreciente y cóncava hacia abajo.
Criterio de la segunda derivada
- Calcular la segunda derivada de la función f(x).
- Identificar los valores de «x» donde la segunda derivada se anula o no existe.
- Aplicar el criterio: si la segunda derivada cambia de signo de positivo a negativo o viceversa en un punto
, entonces
es un punto de inflexión. Si
luego
cóncava hacia arriba, en cambio si
cóncava hacia abajo.
Análisis del gráfico de la función
- Gráfica la función f(x) en un sistema de coordenadas cartesianas.
- Observar la curvatura de la función en diferentes intervalos e identificar los puntos donde cambia su concavidad.
- Criterio: los puntos donde la curvatura cambia de cóncava hacia arriba a cóncava hacia abajo, o viceversa corresponde a los puntos de inflexión.
En resumen, para identificar los puntos de inflexión de una función f(x), se puede evaluar lo que sucede en la función, la primera derivada y la segunda derivada, como se muestra en la tabla siguiente:
|
|
|
|
| Positivo a Negativo | Creciente a Decreciente | Concavidad hacia arriba |
| Negativo a Positivo | Decreciente a Creciente | Concavidad hacia abajo |
Ejercicio resuelto
Para la función
Ver solución
1 – Hallar la primera derivada de la función original:
2 – Se halla la segunda, esta se calcula a partir de la primera derivada ():
3 – Igualar la segunda derivada a 0 (cero):
4 – Encontrar los valores donde (x) de la segunda derivada cambia de signo:
5 – Hallar el punto de inflexión. Para esto se sustituye el valor de (x) en la función original:
Si la segunda derivada cambia de signo en x=0, entonces (0,\ f\left(0\right)) será un punto de inflexiónf\left(0\right)=0.
6 – Gráfica:
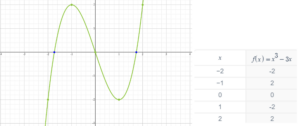
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana