Enciclopedia Iberoamericana
Contenidos
Múltiplos de 9
Número que se puede obtener al multiplicar 9 por otro número entero.
Definición
Un múltiplo de 9 es un número que se puede obtener al multiplicar 9 por otro número entero.
En otras palabras, es un número que contiene al 9 como un factor, siendo un múltiplo positivo si el entero es positivo y cuando se multiplica por 9 un entero negativo, se obtiene un múltiplo negativo.
Estos múltiplos, son el resultado de la tabla de multiplicar del 9. Entonces, 9, 18, 27, 36, 45, y así sucesivamente, son todos múltiplos de 9 porque se obtienen al multiplicar 9 por un número entero.
Ejemplos:
- 9 x 1 = 9
- 9 x 2 = 18
- 9 x 3 = 27
- 9 x 4 = 36
- 9 x 5 = 45
Para representar los múltiplos de 9 se hace de la siguiente manera:
Otra forma interesante de entender estos múltiplos es como una suma sucesiva de 9.
Tan sólo se requiere sumar 9, tantas veces como sea necesario, comenzando evidentemente desde el número 9.
Por esta razón, se dice que un múltiplo de 9 contiene el número 9 «n» veces.
Entonces, los múltiplos de 9 pueden ser vistos como una serie de sumas sucesivas de 9, donde cada término añade otro 9 al total.
Esto es útil para comprender cómo se construyen y también puede ser una forma práctica de calcularlos.
Expresión matemática
Matemáticamente, un múltiplo de 9 es cualquier número que se puede denotar con la siguiente expresión:
Donde:
- «n» es el múltiplo
- «k» es un número entero que representa cuántas veces se multiplica 9 para obtener el múltiplo deseado.
| Enésimo múltiplo | Multiplicación | Múltiplo |
| 1° Múltiplo | 9 x 1 | 9 |
| 2° Múltiplo | 9 x 2 | 18 |
| 3° Múltiplo | 9 x 3 | 27 |
| 20° Múltiplo | 9 x 20 | 180 |
| 35° Múltiplo | 9 x 35 | 315 |
De esta manera, cualquier número «n» que sea el producto de , se dice que es múltiplo de 9. Además, permite hallar el enésimo múltiplo.
Características
Los múltiplos de 9 tienen varias características que los hacen interesantes y útiles en matemáticas. Aquí presentamos algunas de ellas:
- Divisibilidad: todos los múltiplos de 9 son divisibles por 9 sin dejar residuo.
- Suma de sus dígitos es múltiplo de 9: la suma de los dígitos de cualquier múltiplo de 9 también es un múltiplo este. Por ejemplo, la suma de los dígitos de 315 es 3 + 1 + 5 = 9, que es divisible por 9.
- Patrón de repetición en la suma: la diferencia entre cualquier par sucesivo de múltiplos es constante y en este caso, esa constante es 9. Por ejemplo, 36 = 9 + 9 + 9 + 9 (4 veces).
- Relación con la tabla de multiplicar: cada múltiplo de 9 se puede obtener multiplicando 9 por un número entero.
- Suma de sus múltiplos: la suma de varias cantidades múltiplos de 9, es otra cantidad múltiplo de dicho número. Por ejemplo, 45 + 27 = 72.
- Resta de sus múltiplos: la diferencia de dos cantidades múltiplos de 9, es otra cantidad múltiplo de este. Por ejemplo: 90 – 27 = 63.
Cálculo
Multiplicar por 9
La manera más sencilla de calcular un múltiplo de 9 es multiplicando cualquier entero por 9.
Se hace utilizando la expresión matemática mencionada anteriormente: 
| 9 x 1 = 9 | 9 x 2 = 18 | 9 x 3 = 27 |
| 9 x 10 = 90 | 9 x 11 = 99 | 9 x 12 = 108 |
Divisibilidad entre 9
Un método para saber si un número es múltiplo de 9, consiste en dividir el entero dado entre 9. Si la división es exacta, entonces el número es un múltiplo de 9.
Aquí el proceso de manera más detallada:
- División: se toma el número que se está evaluando, por ejemplo 108.
- Dividir entre 9: 108 ¸ 9 = 12.
- Verificar el residuo: Si el resultado de la división es un número entero, es decir, no hay residuo, entonces el número es múltiplo de 9.
| 108 | 9 |
| 19 | 12 |
| -0- |
Por criterio de divisibilidad
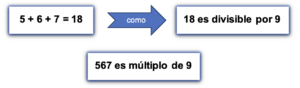
Esta regla establece que un número es divisible por 9 si la suma de sus dígitos resulta un número divisible por 9.
Por ejemplo, si se considera el número 567, la suma de sus dígitos es:
Ejemplos
Algunos ejemplos de múltiplos de 9 son:
| 9 | 18 | 27 | 36 |
| 45 | 54 | 63 | 72 |
| 81 | 90 | 99 | 108 |
| 117 | 126 | 135 | 144 |
Ejercicios de ejemplo
Ejercicio #1
Comprobar si el número 5229 es múltiplo de 9 utilizando el criterio de divisibilidad.
Ver solución
Paso 1: Sumar los dígitos del número: 5 + 2 + 2 + 9 = 18
Paso 2: Evaluar si el resultado de la suma es divisible por 9
18 ÷ 9 = 9 con residuo igual a 0.
Como la suma de los dígitos del 5229 es divisible por 9, entonces el número 5229 es múltiplo de 9 según el criterio de divisibilidad.
Ejercicio #2
¿Cuál es el siguiente múltiplo de 9 después de 54?
Ver solución
Una manera sencilla de hallar el siguiente múltiplo de 54 es sumando 9 a este número: 54 + 9 = 63.
Por lo tanto, el siguiente múltiplo de 9 del entero dado es 63.
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.