Contenidos
División
Operación básica de la matemática que permite distribuir un todo en partes iguales.
Definición
La división es una operación básica de la matemática que permite distribuir un todo en partes iguales, siendo la operación inversa de la multiplicación.
La distribución en partes iguales de un todo de manera exacta no siempre ocurre, pueden sobrar algunos elementos que a su vez deben dividirse para poder ser repartidos o simplemente dejarlos sin repartir.
De este ejemplo sencillo se puede entender las divisiones: se tienen 6 hot dogs para repartir entre dos personas, haciendo la división en partes iguales a cada persona le corresponden 3 hot dogs.

Por ser la división la operación inversa de la multiplicación, al dividir se halla uno de los factores de la multiplicación. Además, por ser inversa mediante la multiplicación se puede comprobar que el resultado de una división sea correcto.
Según el ejemplo, hay dos personas y a cada una le corresponden 6 hot dogs, si se desea saber cuántos hot dogs hay entre las 2 persona se multiplica 2 x 3 = 6, que fue la cantidad que se tenía inicialmente para repartir.
Partes
La división tiene varios elementos que la conforman con nombres propios cada uno de ellos. Siempre se pueden diferenciar uno del otro sin importar la manera como se exprese la operación de la división.
Publicidad, continua debajo
- Dividendo (d): el número que se va a dividir, el que se va a repartir.
- Divisor (D): el número que divide al dividendo, e indica entre cuantas partes se desean repartir los elementos.
- Cociente (c): resultado de una división.
- Residuo (r): es el número que sobra cuando se divide un número entre otro.
- Signo: la operación de la división suele indicarse con un símbolo al que se denomina óbelo (÷). Sin embargo, también pueden utilizarse dos puntos (:) o una barra inclinada (/).
Tipos
Las divisiones se pueden clasificar en dos tipos y esto depende del resultado del residuo, que este sea igual a cero o diferente de cero.
Divisiones exactas
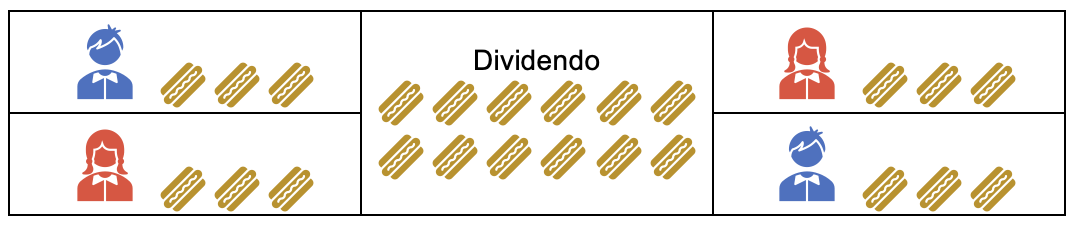
Cuando el residuo es igual a cero. Esto significa que el número de elementos a repartir del dividendo, se hace completamente entre las partes del divisor sin que quede residuo alguno.
Por ejemplo, al dividir 12 ÷ 4 = 3; el cociente o resultado es 3, por lo que los 12 elementos del dividendo se pueden repartir perfectamente entre las 4 partes del divisor, correspondiéndole a cada parte 3 elementos y no sobra nada.
Divisiones inexactas
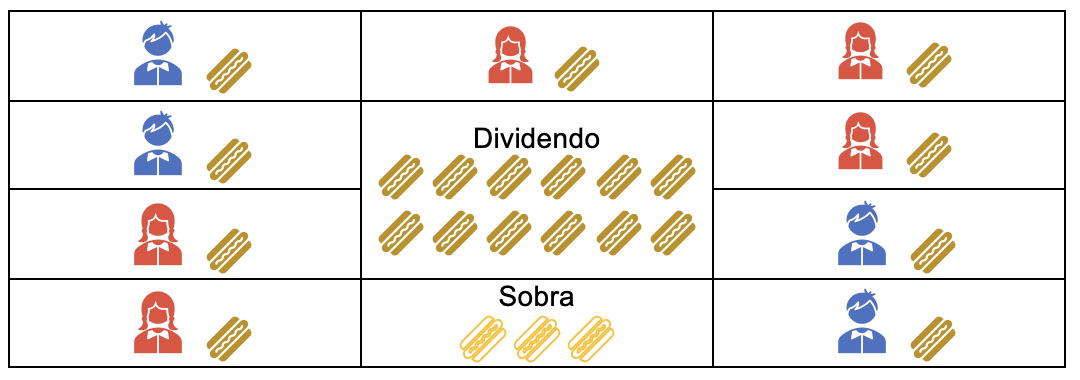
Esta se da cuando el residuo es diferente de cero y menor que el divisor. Es decir, que el número de elementos del dividendo no fue posible repartirlos completamente entre las partes del divisor, quedando elementos sin repartir.
Para este caso, si se tiene 12 ÷ 9 = 1 y sobran siempre 3, y por más que se desee repartir lo que sobró entre las partes del divisor siempre sobraran 3 porciones del elemento.
¿Cómo resolver una división?
Los elementos de la división dan lugar a las llamadas divisiones de una cifra (divisor con un solo dígito), divisiones de dos cifras (divisores de dos dígitos), divisiones con decimales en el dividendo y/o en el divisor.
Se explicarán estos casos con ejemplos para una mejor comprensión.
Divisiones de una cifra
El dividendo puede tener cualquier cantidad de cifras, pero el divisor tiene un solo dígito.
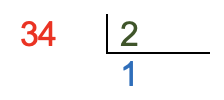
| Se escribe el dividendo del lado izquierdo al separador de la división y el divisor del lado derecho. | |
| Verificar que el primer dígito del dividendo sea igual o mayor al dígito del divisor. Se empieza dividiendo cada cifra del dividendo de izquierda a derecha.
Si es mayor o igual se comienza a dividir ese dígito, en caso contrario que sea menor que el divisor, entonces se consideran los dos primeros dígitos del dividendo. |
|
 |
Como el primer dígito del dividendo es mayor que el divisor, se hace la pregunta ¿cuántas veces cabe el 2 en el número 3?. También se suele preguntar ¿qué número multiplicado por 2 resulta 3 o próximo a 3 sin excederse?
La respuesta es 1, (3 ÷ 2 = 1). El resultado se coloca en el cociente. |
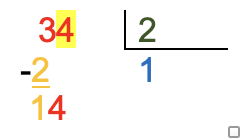 |
Restar el producto del divisor por el cociente (2 × 1) con el dígito del dividendo (3 – 2) y escribe la diferencia a continuación.
Se baja la siguiente cifra del dividendo al lado de la resta que se acaba de hacer. |
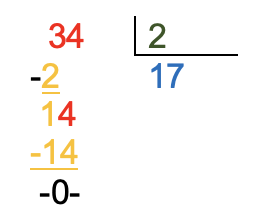 |
Ahora, se realiza la división del nuevo dividendo (14) entre el dígito del divisor (2), realizando las preguntas que se mencionaron en el paso No. 3.
Para este caso 14 ÷ 2 = 7. Y se repiten los pasos 4 y el No. 5 de ser necesario. El residuo resultante es cero, la división es exacta. |
Divisiones de dos cifras
El dividendo puede tener cualquier cantidad de cifras, pero el divisor tiene dos dígitos.
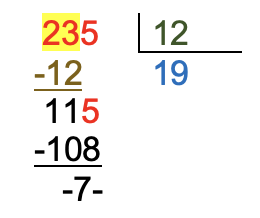 |
|
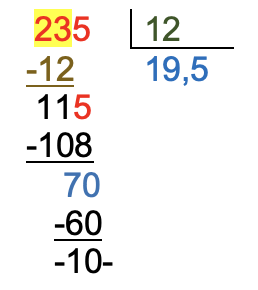 |
|
Divisiones con decimales
Se pueden dar tres casos:
- Un decimal entre un número entero: se dividen como si fueran enteros y al bajar el primer dígito decimal del dividendo, se escribe la coma en el cociente, continuando el proceso de división.
- Un entero entre un decimal: por regla no se puede dividir con un número decimal en el divisor, por tanto, se debe convertir el número decimal en entero y esto se hace multiplicando el divisor por la unidad seguido de tantos ceros como dígitos decimales tenga el número. Para no alterar la división, también se debe multiplicar el dividendo por la misma cantidad que se haya multiplicado el divisor.
- Un decimal entre un decimal: al igual que en el caso anterior, se debe convertir el divisor a un número entero, siguiendo el mismo proceso.
Propiedades
Las principales propiedades de la división son las siguientes:
- Es no conmutativa: en la división no se puede cambiar el orden de los números (dividendo y divisor), debido a que, si se afecta el resultado, entonces de manera general
.
- No es asociativa: esta propiedad refiere que se pueden agrupar de distintas maneras los números y el resultado debe ser el mismo, pero en la división esto no se cumple, siendo
.
- Dividir entre uno: cualquier número dividido entre uno da como resultado el mismo número.
.
- División del cero: al dividir el cero, entre cualquier número, el resultado siempre da igual a cero.
.
Ejemplos
Algunos ejemplos de división son:
| 15 ÷ 3 = 5 | 55,5 ÷ 8 = 6,93 | 99 ÷ 3 = 33 | 100 ÷ 40 = 2,5 |
| -52 ÷ 3 = 17,33 | 8 ÷ 3 = 2,66 | 74 ÷ 9 = 8,22 | 1554 ÷ 63 = 24,66 |
| -36 ÷ -6 = 6 | 10 ÷ 10 = 1 | 0 ÷ 1 = 0 | 223 ÷ 10 = 22,3 |
Ejercicios resueltos
Ejercicio #1
Operación a realizar: realizar la división de un número decimal entre un entero. 92,3 ÷ 8.
Ver solución

El resultado de la operación es 11,5.
Ejercicio #2
Operación a realizar: realizar la división siguiente: 576 ÷ 2,6.
Ver solución
Primero se deben eliminar los decimales del divisor, multiplicándose por la unidad seguido de un cero, ya que solo hay un dígito decimal.
2,6 x 10 = 26.
Seguidamente para no alterar la división se multiplica el dividendo también por 10 (576 x 10 = 5760). Ahora se divide según el proceso conocido.
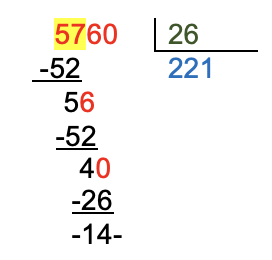 El resultado de la operación es 221.
El resultado de la operación es 221.
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana