Contenidos
Propiedad asociativa
Propiedad que establece que el orden en el cual se agrupen los números o términos en una suma o multiplicación no altera el resultado.
Definición
La propiedad asociativa establece que el orden en el cual se agrupen los números o términos en una suma o multiplicación no altera el resultado.
Mediante la propiedad asociativa se pueden asociar términos para facilitar ciertos cálculos en aritmética y álgebra, esta agrupación de los términos se realiza en el orden que se desee y el resultado siempre será el mismo.
Algunas características de aplicación de la ley asociativa, como también se le conoce, son las siguientes:
- Para la agrupación de números o términos se hace uso de paréntesis o corchetes.
- La propiedad asociativa se aplica a la suma y multiplicación del conjunto de números
,
,
,
,
.
- Los números que se agrupan dentro de un paréntesis o corchete se convierten en una unidad.
- La propiedad asociativa solo se aplica a las operaciones matemáticas de la suma y la multiplicación y no con la resta o la división.
- La aplicación de la ley asociativa resulta mucho más útil cuando se combina con la propiedad conmutativa.
Propiedad asociativa de la suma
En la suma se puede aplicar la propiedad asociativa, para este caso la ley asociativa indica que la suma de tres o más números es el mismo sin importar cómo se agrupan los sumandos.
A manera de fórmula se puede expresar que sean a, b, c números de cualquier conjunto de números se cumple que:
En la realización de números con diferentes signos resulta muy útil aplicar la ley asociativa en combinación con la propiedad conmutativa, ya que conviene agrupar los números de igual signo para hallar su resultado y simplificar la operación.
Publicidad, continua debajoPor ejemplo, si se tiene la operación matemática: (-3) + 9 (-5)
[(-3) + 9] + (-5) = (-3) + [9 + (-5)]
6 – 5 = – 3 + 4
1 = 1
En combinación con la propiedad conmutativa se pueden agrupar los números de signo negativo y luego operar con el número de signo positivo, de la manera siguiente: (-3) + 9 (-5) = [(-3) + (–5)] + 9 = (-8) + 9 = 1.
Para cualquiera de los casos el resultado de la suma es el mismo.
Propiedad asociativa de la multiplicación
En la multiplicación la propiedad asociativa establece que el producto de tres o más números permanece igual independientemente de la forma en que se agrupen los factores.
De manera general se tiene que para a, b, c, que pertenezcan a cualquiera del conjunto de números conocidos (,
,
,
,
) se cumple que:
(a * b) * c = a * (b * c)
La propiedad asociativa es útil al multiplicar varios números, ya que se pueden crear varias asociaciones de números más pequeños para resolver la operación matemática.
Operaciones matemática no asociativas
Las operaciones básicas de la matemática como la resta y la división se consideran «no asociativas», es decir, que la propiedad asociativa no se cumple en dichas operaciones matemáticas.
Resta
En la resta . Con un ejemplo se puede comprobar que la ley asociativa no se cumple en la resta. Se debe recordar que se trata de una resta y no de una suma de números de diferentes signos.
18 – 5 – 6 = (18 – 5) – 6 = 13 – 6 = 7
18 – 5 – 6 = 18 – (5 – 6) = 18 – (-1) = 18 + 1 = 19
Al agrupar los términos de diferentes maneras, se obtienen diferentes resultados que anulan la aplicación de la propiedad asociativa en la resta.
División
En la división se tiene que . Así para las divisiones
72 ÷ 4 ÷ 2, al asociar los dos primeros números se tiene:
(72 ÷ 4) ÷ 2 = 18 ÷ 2 = 9.
Ahora al asociar los dos últimos números resulta:
72 ÷ (4 ÷ 2) = 72 ÷ 2 = 36.
Por tanto (72 ÷ 4) ÷ 2 ≠ 72 ÷ (4 ÷ 2), no se cumple la propiedad asociativa
Ejercicio resueltos
Problema a resolver: en una bodega se tienen almacenadas 12 cajas de vino, cada caja contiene 6 botellas. Si cada botella se vende en 10 dólares ¿Cuánto se obtendrá por la venta de todas las botellas de vino?
Ver solución
Para resolver el problema se realiza una multiplicación que consiste en multiplicar las 12 cajas por las 6 botellas de vino que contiene cada caja, así se podrá conocer el número total de botellas de vino.
Luego este resultado se multiplica por el valor de cada botella, de esta manera se hallará el valor total que se obtendrá de la venta
Se puede hacer una representación gráfica del problema para su mejor entendimiento.
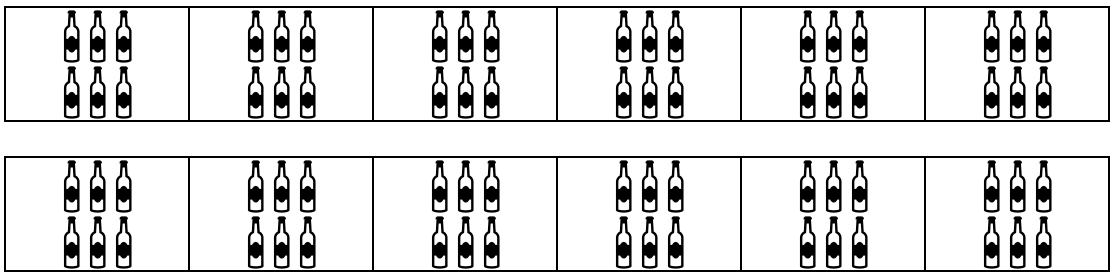
(12 * 6) * 10 = 72 * 10 = 720 dólares
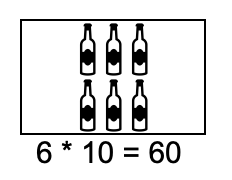
Otra manera de resolver el problema es multiplicar las 6 botellas de vino por los 10 USD que vale cada botella y luego, multiplicar por las 12 cajas.
12 * (6 * 10) = 12 * 60 = 720 USD
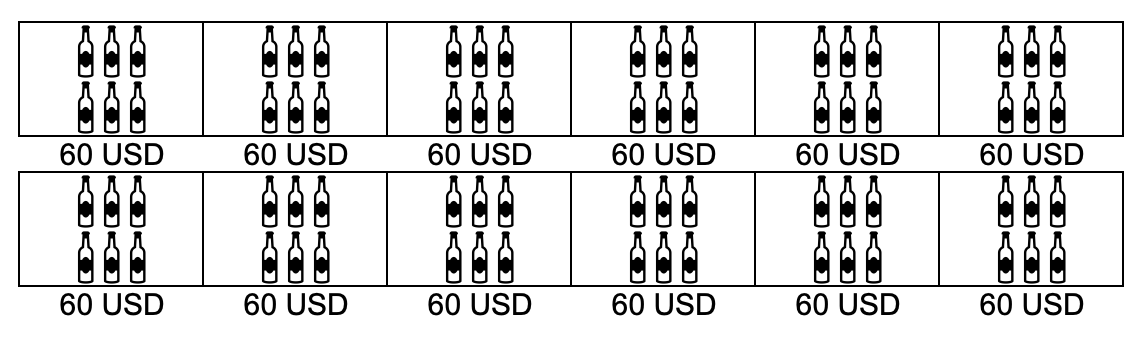
De esta manera se resuelve el problema y se verifica que se cumple la propiedad asociativa.
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana