Contenidos
Propiedad distributiva
Propiedad que permite tomar un factor y distribuirlo a cada miembro de un grupo de elementos que se encuentran sumándose o restando.
Definición
La propiedad distributiva, en una de las reglas elementales en aritmética y álgebra y relaciona una suma o resta con respecto a una multiplicación o división. Aunque para la división existen ciertas características que se deben cumplir.
Esta propiedad, por ejemplo, permite tomar un factor y distribuirlo a cada miembro de un grupo de elementos que se encuentran sumándose o restando. En vez de multiplicar el factor por todo el grupo como un todo, se puede distribuir para que sea multiplicado por cada miembro del grupo individualmente.
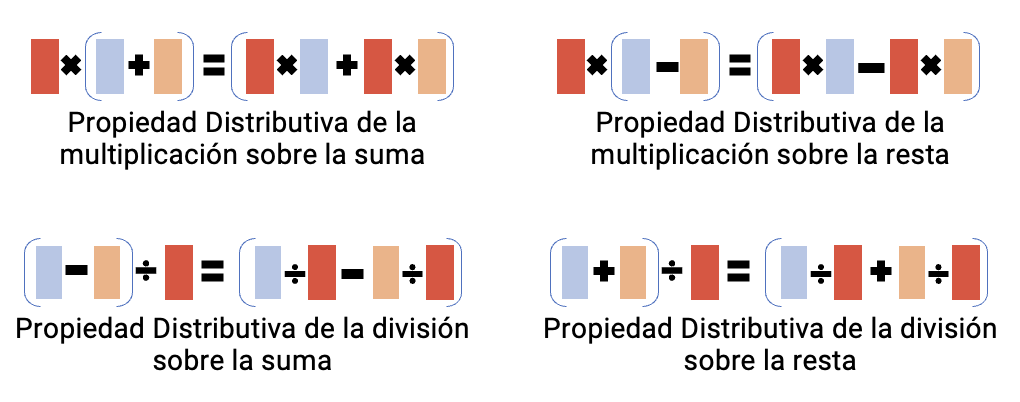
Entonces, esta propiedad combina dos operaciones que pueden ser: la multiplicación con la suma, la multiplicación con la resta, la división con la suma o la división con la resta.
La propiedad distributiva es una forma práctica de reorganizar expresiones aritméticas o algebraicas, utilizada en operaciones en las cuales su aplicación hará más fácil su cálculo.
Esto es, porque se puede distribuir el factor de varios dígitos en una «suma de grupo» y luego distribuir el otro factor a los miembros de ese grupo.
La propiedad distributiva funciona para grupos de suma o resta de cualquier tamaño, incluso para operaciones combinadas.
Publicidad, continua debajoPropiedad distributiva de la multiplicación sobre la suma
Este caso de aplicación de la propiedad distributiva es más conocida y hace referencia a la multiplicación en combinación con la suma. De manera general se expresa como:
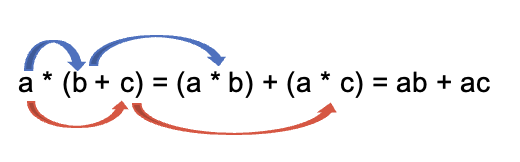
La propiedad es distributiva sobre la suma tanto a la derecha como a la izquierda: a * (b + c) o también se puede aplicar en (b + c) * a.
De esta manera se está distribuyendo la multiplicación entre todos los miembros de un grupo que se están sumando.
Al aplicar esta propiedad se debe cumplir que la suma de dos números multiplicados por un tercer número es igual al producto de cada sumando por separado por el mismo tercer número y luego sumar los resultados para obtener una cifra total.
Ejemplificado con número enteros se tiene que:

Es importante aclarar que es la multiplicación la que se distribuye con respecto a la suma y no al contrario. Así de esta manera, no se aplica la propiedad distributiva sobre la suma en casos como: a + (b * c) → 5 + (3 * 6). En esta operación no aplica la propiedad y para resolverla primero se halla el producto dentro del paréntesis y luego se realiza la suma: 5 + (3 * 6) = 5 + 18 = 23.
Propiedad distributiva de la multiplicación sobre la resta
La propiedad distributiva de la multiplicación sobre la resta es similar a la propiedad distributiva de la multiplicación sobre la suma, pero en este caso se restan los productos obtenidos.
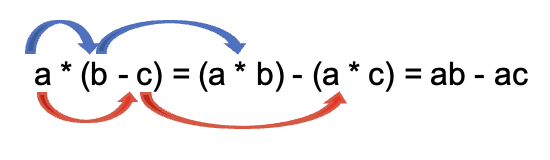
La razón por la que también funciona para la resta, es debido a que esta es la operación inversa de la suma.
La propiedad es distributiva sobre la suma tanto a la derecha como a la izquierda: a * (b – c) o también se puede aplicar en (b – c) * a.
De manera general, se debe cumplir que la diferencia de dos números por el producto de un tercer número es igual a la diferencia de cada número por el producto mismo tercer número.
5 * (7 – 4) = (5 * 7) – (5 * 4) = 35 – 20 = 15
5 * (7 – 4) = 5 * 3 = 15
Propiedad distributiva en la división
La propiedad distributiva en la división se cumple cuando el número que se distribuye, es decir; el que está fuera del paréntesis está como divisor.
Entonces, la propiedad distributiva de la división con respecto a una suma o resta, se cumple cuando la adición o la sustracción actúan como dividendo y el número fuera del paréntesis se encuentra como divisor.
- Propiedad distributiva de la división con respecto a la suma: aplicando la propiedad se resuelve de la manera siguiente: (a + b) ÷ c = a ÷ c – b ÷ c. El orden de precedencia de las operaciones matemáticas indica que primero se resuelven las divisiones y luego la suma.
- Propiedad distributiva de la división con respecto a la resta: para este caso la propiedad se resuelvmue: (a + b) ÷ c = a ÷ c – b ÷ c. El orden de precedencia de las operaciones matemáticas indica que primero se resuelven las divisiones y luego la resta.
Como se comentó, la propiedad es distributiva en la división respecto a la suma o la resta sólo a la izquierda, por lo que no aplica cuando se tiene el caso: a ÷ (b ± c).
Utilizando un ejemplo se verificará lo mencionado:
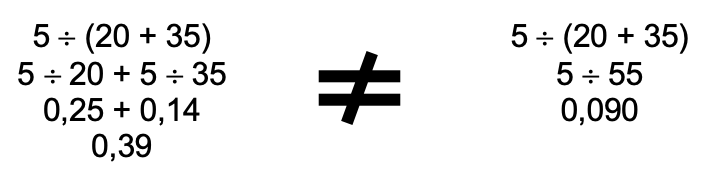
Ahora, se comprobará que la propiedad si aplica hacia la izquierda:
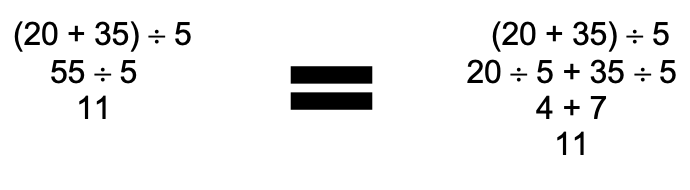
Propiedad distributiva en el álgebra
En álgebra, la propiedad distributiva se aplica de igual manera que en la aritmética, es decir; que, con números pertenecientes a cualquier conjunto conocido ,
,
,
,
.
Es de gran utilidad, debido a que con su aplicación se pueden simplificar expresiones algebraicas.
Por ejemplos, si se tiene la siguiente operación: 3 * (x + 2), el grupo entre paréntesis (x + 2) no se puede simplificar como una operación aritmética. En este caso se deja la expresión tal como está o se aplica la propiedad distributiva.
Aplicando la propiedad se tendría: 3*(x + 2) = 3*x + 3*2 = 3x + 6.
Ejercicios resueltos
Aplicar la propiedad distributiva en cada uno de las siguientes operaciones y verificar que se cumpla la propiedad.
- 4 * (5 – 2 + 3)
- (5x + 4 + x) * x
- (20 – 3) * 2
Ver solución
|
4 * (5 – 2 + 3) 4 * 6 24 |
= |
4 * (5 – 2 + 3) 4*5 – 4*2 + 4*3 20 – 8 + 12 24 |
Lo que está dentro del paréntesis es una suma de números enteros de diferentes signos. Se cumple la propiedad. |
|
(5x + 4 + x) * x (6x + 4) * x 6x2 + 4x No se puede simplificar más |
= |
(5x + 4 + x) * x 5x2 + 4x + x2 6x2 + 4x |
Lo que está dentro del paréntesis es una suma de números enteros de diferentes signos. Se cumple la propiedad |
|
(20 – 3) * 2 17 * 2 34 |
= |
(20 – 3) * 2 20*2 – 3*2 40 – 6 34 |
Lo que está dentro del paréntesis es una suma de números enteros de diferentes signos. Se cumple la propiedad |
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana