Contenidos
Multiplicación
Operación aritmética que consiste en calcular el resultado de la suma de un mismo número, tantas veces como lo indique otro número.
Definición
La multiplicación es una operación básica aritmética, que se origina, desde su forma más simple de la suma sucesiva de un mismo número.
Es conocida como una suma abreviada, ya que su proceso consiste en calcular el resultado de la suma de un mismo número (multiplicando), tantas veces como lo indique otro número (multiplicador).
Con un ejemplo se puede comprender este proceso de multiplicación. Supóngase que hay un colegio con 5 salones de clase y que en cada salón hay 12 estudiantes, para saber, cuántos estudiantes hay en total, se podrían agrupar todos y contarlos.
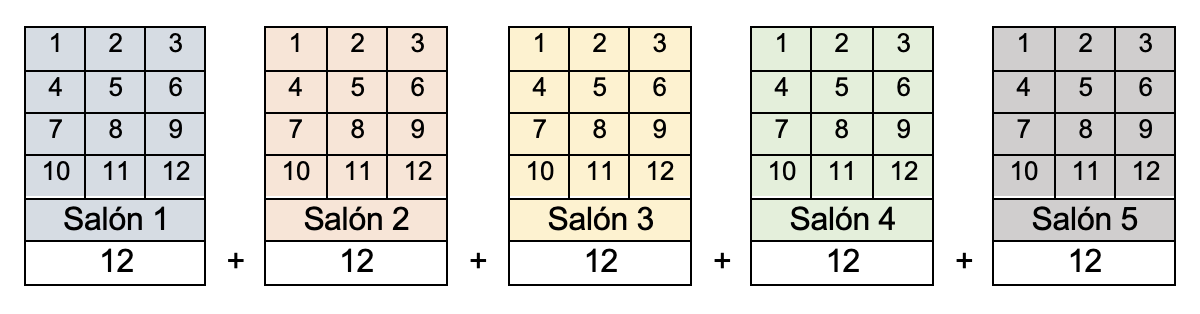
Otra manera, es sumar 5 veces el 12 de este modo: 12 + 12 + 12 + 12 + 12 = 60. En total hay 60 estudiantes o simplemente se abrevia la suma sucesiva para convertirla en una multiplicación 12 x 5, que refiere sumar 5 veces el 12.
Ahora, ¿por qué usar la multiplicación si es lo mismo que una suma repetida? La respuesta es, debido a que la multiplicación permite simplificar la suma, principalmente cuando se trata de números más grandes.
Considere en el ejemplo anterior, tener quizás, que conocer el número de estudiantes de 25 colegios cada uno con 5 salones y de 12 estudiantes, sería una suma demasiado extensa, por lo que conviene realizar una multiplicación.
Publicidad, continua debajoAsí, la multiplicación tiene su aplicación fundamental en el cálculo de cantidades, medidas, en procesos donde las cantidades cambian constantemente de valor.
Propiedades
En matemática se han definido diferentes propiedades para la multiplicación, que permiten aplicarlas para facilitar la realización de la operación matemática.
Estas propiedades se aplican a cualquier conjunto de números conocidos, naturales, enteros, racionales, reales y complejos, además de expresiones algebraicas, entre otros.
A continuación, se definen cada una de las propiedades de la multiplicación:
- Propiedad conmutativa: esta propiedad refiere, que no importa el orden en el que se multipliquen los números, siempre se obtendrá el mismo resultado. Se puede tener 5 * 4 = 20 o bien 4 * 5 = 20.
- Propiedad asociativa: si se deben multiplicar más de tres números, estos se pueden agrupar de distintas maneras para facilitar los cálculos y el resultado final será el mismo. Así, si se tienen los números representados con las letras a, b, c se pueden multiplicar de varias maneras:
Lo que se encuentra entre paréntesis se debe multiplicar primero y el resultado se multiplica por el otro número. Por ejemplo
(2 * 3) * 5 = 6 * 5 = 30, se puede realizar de la manera:
2 * (3 * 5) = 2 * 15 = 30. El resultado es el mismo. - Propiedad del elemento neutro: es también conocida como propiedad modulativa. Esta define, que todo número multiplicado por el número 1 es igual al mismo número. Multiplicar 213 * 1 = 213. 78 * 1 = 78. El elemento neutro de la multiplicación es el número 1 y se puede generalizar la propiedad como: a * 1 = a
- Propiedad absorbente: en esta propiedad cualquier número que se multiplique por 0, dará como resultado el número 0. Por ejemplo, 12 * 0 = 0, 310 * 0 = 0.
- Propiedad distributiva: en esta propiedad se hace referencia a la multiplicación en combinación con la suma o resta, de la siguiente manera:
Si se tiene la siguiente multiplicación 5 * (2 + 6), para resolver se multiplica el número que está fuera del paréntesis por cada número dentro del paréntesis y luego se suman los resultados.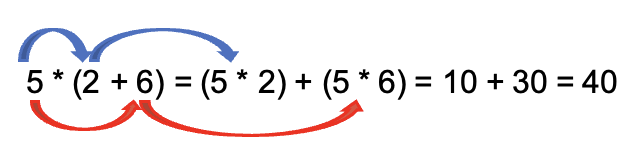 Se puede generalizar de la siguiente manera: a * (b ± c) = a*b ± a*c, el signo ±, significa que se puede dar una suma o una resta, pero el proceso es el mismo.
Se puede generalizar de la siguiente manera: a * (b ± c) = a*b ± a*c, el signo ±, significa que se puede dar una suma o una resta, pero el proceso es el mismo.
Partes
La operación de la multiplicación tiene varios elementos que la componen:
- Factores: que son los números que se multiplican entre sí. Los factores tienen nombres específicos, uno es el “multiplicando” que es el número que se va a multiplicar y el “multiplicador” que indica las veces que se suma el multiplicando.
- Producto: es el resultado de la multiplicación.
- Signo: hay diferentes formas de representarlo, ya sea con una cruz o equis (x) o con un asterisco (*). El signo separa cada uno de los factores de la multiplicación e indica qué operación se debe realizar.
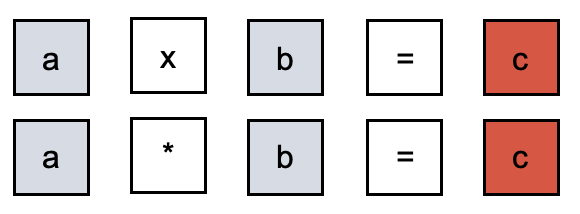
Donde “a” y “b” son los factores y “c” el producto. Especificando los factores se tiene que “a” es el multiplicando y “b” el multiplicador.
Resolver una multiplicación
Partiendo de los elementos básicos de la multiplicación se explicarán los pasos para su resolución.
Desde la definición de la multiplicación de dos números, se puede desarrollar la multiplicación que sigue a continuación. Los factores se pueden ordenar de manera vertical o horizontal.
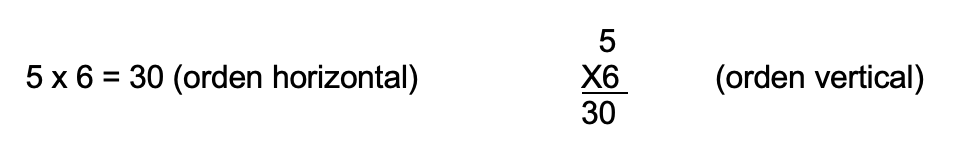
De esta manera se tiene que, para multiplicar 5 x 6, es igual a sumar el 5 repetidamente 6 veces, 5 + 5 + 5 + 5 + 5 + 5= 30, entonces se tiene que 5 x 6 = 30.
Estas multiplicaciones básicas de dos números naturales, se resumen en lo que se conoce como la tabla de multiplicar, una vez aprendidas se pueden hacer multiplicaciones más largas como la siguiente.
Se tiene la multiplicación de 1243 x 2. Se multiplica cada número del multiplicando (1243) por el multiplicador (2).
Primero se alinean los números de manera vertical, ordenándolos por su valor posicional, unidad, decena, centena, unidad de mil. Y se escribe el signo a la izquierda del multiplicador.
Una vez ordenados se traza una línea para separar los factores de los que será el producto o resultado.
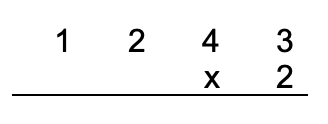
Luego, se multiplica cada dígito del multiplicando por el multiplicador, comenzando desde la unidad y en orden, cada resultado obtenido se escribe debajo de la línea que se trazó, de igual manera en orden de posición de cada dígito.
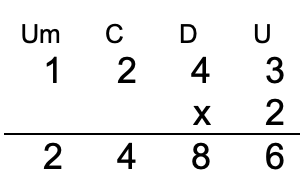 |
|
Si el resultado de una de las multiplicaciones tiene dos cifras, por ejemplo 15, se escribe el dígito de la unidad y el de la decena se coloca sobre la cifra del número siguiente de la izquierda y se suma al producto de ese renglón.
En el caso que el multiplicador tenga más de dos dígitos, se realiza el proceso anterior, el multiplicando por el dígito de la unidad del multiplicador, luego se procede a multiplicar el multiplicando por el dígito de la decena del multiplicador corriendo un lugar hacia la izquierda en el resultado. Por último, los resultados se suman.
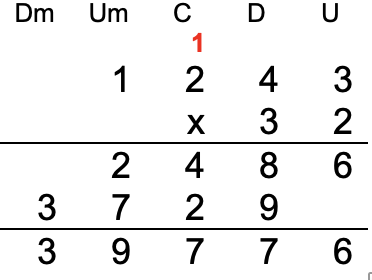 |
|
Ejemplos
Algunos ejemplos de multiplicación son:
| 4 x 4 = 12 | 18 x 5 = 90 | 9 x 4 = 36 | 5 x 5 = 25 |
| 3 x 1 = 3 | 200 x 3 = 600 | 100 x 100 = 10000 | 16 x 3 = 48 |
| 5 x 7 = 35 | 2 x 2 = 4 | 1 x 188 = 188 | 173 x 0 = 0 |
Ejercicios resueltos
Ejercicio #1
Problema a resolver: en las siguientes operaciones indicar que propiedad de la multiplicación se aplicó.
| Multiplicación | Solución |
| 2 x 3 = 3 x 2 | |
| 762 x 1 | |
| 23 x (3 x 3) | |
| 9834 x 0 | |
| 11 x (21 – 9) |
Ver solución
| Multiplicación | Solución |
| 2 x 3 = 3 x 2 | Propiedad conmutativa |
| 762 x 1 | Elemento neutro |
| 23 x (3 x 3) | Propiedad asociativa |
| 9834 x 0 | Propiedad absorbente |
| 11 x (21 – 9) | Propiedad distributiva con respecto a la resta |
Ejercicio #2
Problema a resolver: resolver las siguientes operaciones
- 3 x 12
- 4 + 3 x 2
- 10 x 3
Ver solución
Punto a)
El resultado de 3 x 12 es el equivalente a repetir 12 veces 3, por lo tanto es igual a 36.
3 x 12
3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3 + 3
36
Punto b)
Al haber un signo + es necesario separar en términos, por lo que el cálculo queda como 4 + (3 x 2), lo que es igual a:
4 + (3 x 2)
4 + (3 + 3)
4 + 6
10
Punto c)
El resultado de 10 x 3 es el equivalente a repetir 3 veces 10, por lo tanto es igual a 30.
10 x 3
10 + 10 + 10
30
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana