Teorema del seno

Definición

El teorema del seno tiene su aplicación para hallar las medidas de longitudes o ángulos que faltan en un triángulo oblicuo, si se conocen dos de los ángulos y uno de sus lados.

Para entender con facilidad la formulación del teorema del seno, se utiliza la representación gráfica del triángulo  de la figura denotado como ABC, cuya amplitud de sus ángulos son α, β, δ  y las longitudes de sus lados opuestos son a, b, c; respectivamente.

Entonces, ley del seno se enuncia como:

“En cualquier triángulo las longitudes de los lados son proporcionales a los senos de los ángulos opuestos correspondientes”

Al encontrar el ángulo desconocido de un triángulo cualquier, la fórmula de la ley de los senos se puede escribir como:

Esta relación permanece igual para los tres lados y ángulos opuestos de cualquier triángulo.

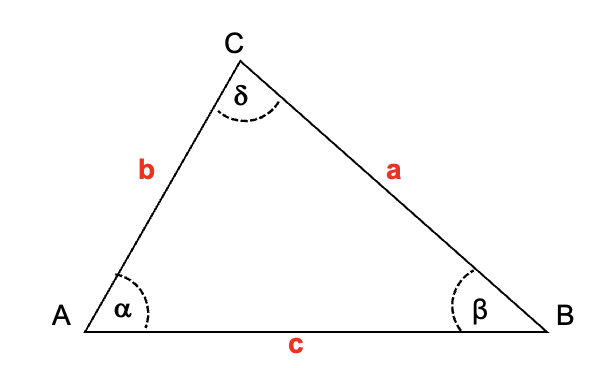
Esta fórmula se puede representar en otras formas diferentes a la dada. Si se desea calcular la medida de los lados la proporción se expresa como:

Casos de uso

Como se mencionó, la ley del seno está determinado para hallar ángulos o lados de un triángulo donde no es posible usar las fórmulas definidas para los triángulos rectángulos.

Sin embargo, este teorema se puede usar si se dan ciertas combinaciones de medidas en un triángulo.

Hay dos casos específicos para esta situación:

• Criterio LAA: cuando se conocen dos ángulos y un lado para encontrar otro lado desconocido. Esta técnica se conoce como triangulación.
• Criterio LLA: dado dos lados y el ángulo opuesto a uno de esos lados.

Otros casos diferentes para triángulos oblicuos, se emplea el teorema del coseno.

Resolución

Para calcular la longitud de un lado del triángulo cualquiera

Si necesita calcular la longitud de un lado, es necesario usar la relación de la ley del seno en la cual las longitudes están en la parte superior de la fórmula.

Por ejemplo; si se tiene el siguiente triángulo como se muestra en la figura, del cual se conocen sus ángulos a, b y el lado “a”, y se desea conocer el lado “x”.

1. Paso 1. Identificar la información suministrada y que se desea calcular.
2. Paso 2. Escribir la fórmula de la ley del seno que relaciona los datos obtenidos y a calcular. Cada fracción en la fórmula debe contener un lado y su ángulo opuesto.
3. Paso 3. Sustituir los valores.
4. Paso 4. Despejar la variable
5. Paso 5. Resolver la ecuación resultante para encontrar el lado desconocido.

Para hallar la amplitud de un ángulo, debe usar la fórmula donde los ángulos están en la parte superior. Por ejemplo; para encontrar el ángulo en el vértice “A”, conocidos el la medida de ∠β y los lados “a” y “b”.

Los pasos son los indicados en el caso anterior, con la diferencia de la relación del teorema a usar.

Ejercicios de ejemplo

Ejercicio #1

Calcular el valor del lado “b” de la figura.

Ejercicio #2

Hallar los valores de los lados y ángulos del triángulo de la figura.