Enciclopedia Iberoamericana
Contenidos
Regla de Ruffini
Método utilizado en álgebra para realizar la división de un polinomio.
Definición
La Regla de Ruffini es un método utilizado en álgebra para realizar la división de un polinomio D(x) entre un binomio de la forma (x ± a), donde (a) es un número real.
Este método proporciona una forma eficiente de encontrar el cociente y el residuo de la división, sin la necesidad de realizar la división completa utilizando la tradicional división larga de polinomios.
A la regla de Ruffini, también se le conoce como método de Ruffini o división sintética.
En términos más específicos, la Regla de Ruffini utiliza un arreglo o tabla simplificada que facilita el proceso de dividir un polinomio por (x ± a).
El procedimiento implica evaluar el polinomio en (a), utilizando los coeficientes del polinomio original de manera sistemática para encontrar los coeficientes del cociente y el residuo.
Elementos
Para la aplicación de la regla de Ruffini se deben identificar los elementos de la división:
- Divisor: que es un binomio de grado 1 que divide al polinomio original.
- Dividendo: es el polinomio que se desea dividir por el divisor.
- Cociente: es el resultado de la división, que se expresa como un nuevo polinomio de grado menor al dividendo.
- Residuo: es el resto de la división, que es un número real.
Procedimiento
Para comprender como es el procedimiento para dividir polinomios aplicando la Regla de Ruffini se realizará con el siguiente ejemplo:
Se desea dividir el polinomio 
- Verificar que el divisor cumpla con el parámetro
. Para el caso, se cumple ya que
- Se ordena el polinomio dividendo en orden decreciente (de mayor a menor grado). Si falta algún término, se debe completar con un coeficiente de 0.
- Se escriben los coeficientes del polinomio dividendo
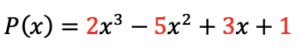en una tabla como las que se indican:
- A la izquierda se escribe el término independiente del divisor (a) con signo opuesto. En este caso
- Se comienza a realizar la división bajando el primer coeficiente (el de grado mayor) a la tercera fila de la tabla.
- Se multiplica el coeficiente bajado
por el divisor que es el término (a = 2) y el resultado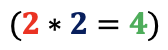 
se escribe en la segunda fila debajo del siguiente coeficiente y se realiza la operación aritmética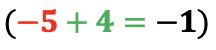 
Considere:- Los números en la segunda fila se obtienen multiplicando el divisor por el número que se obtuvo en la tercera fila.
- Los números en la tercera fila se obtienen al realizar la operación aritmética de los números de la primera y segunda fila.
- Se repite el paso anterior, pero ahora se multiplica el divisor (2) por el número obtenido de la operación aritmética (-1). Esto se hace hasta completar paso a paso la tabla.
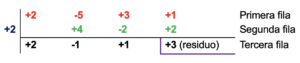
El último número obtenido en la tercera fila corresponde al residuo de la división y lo demás será el cociente.y el residuo R = 3
- Se escribe el resultado final:
Siguiendo estos pasos de manera ordenada y sistemática, se puede aplicar correctamente la Regla de Ruffini para dividir un polinomio entre
Ejercicio de ejemplo
Se tienen los polinomios: 
Ver solución
Para este ejemplo el valor de a=+1 siendo su opuesto (-1), este será el divisor.
Se puede observar que en el polinomio dividendo no hay el término 
Ahora se procede a realizar la división.
 |
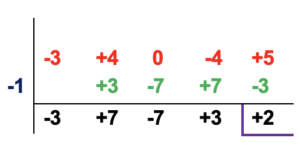Pasos Escribir los coeficientes del dividendo Se escribe el término independiente del divisor Bajar el primer coeficiente Multiplicar el divisor por el coeficiente Realizar la suma de los coeficientes |
El resultado de la división es:
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.