Triángulo

Definición

Un triángulo es una figura geométrica de tipo polígono que se caracteriza por tener tres vértices, tres lados y tres ángulos.

Los vértices del triángulo se denotan con cualquier letra en mayúscula (A, B, D, E,…) y los lados se identifican con la misma letra del vértice opuesto pero, con letra minúscula (a,b,d,e,…), también pueden ser nombrados con las letras de los dos vértices que se unen con el segmento de recta, como .

Por su parte, los ángulos del triángulo se pueden denotar de diferentes maneras, con una letra griega, con la misma letra que el vértice correspondiente o empleando el símbolo , por ejemplo; en la figura el ángulo que está en el vértice D, se denota como 

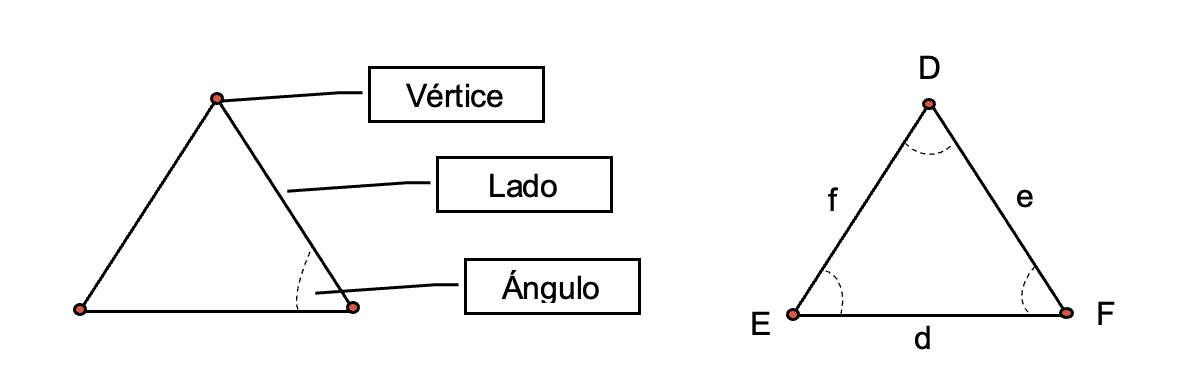
En la figura se observa que:

• Los vértices del triángulo son D, E, F.
• Los lados son: d, e, f. Para la figura en estudio, el lado “d” une los vértices , el lado “e” une los vértices y por último, el lado “f” une los vértices .
• Los ángulos son: , y .

Propiedades

Los triángulos poseen unas propiedades particulares, importantes a considerar para la construcción de un triángulo cualquiera, para realizar cálculos y resolver problemas aplicados a este tipo de figura geométrica.

Entre las propiedades a destacar se encuentran:

• La suma de los tres ángulos internos es igual a 180°. + + = 180°.
• La suma de los tres ángulos externos es igual a 360°
• La longitud de cualquiera de los lados del triángulo debe ser menor a la suma de la longitud de los dos lados restantes. Se entiende: d < (e + f).
• El lado de mayor longitud es opuesto al ángulo interno de mayor amplitud, de igual manera, el lado menor es opuesto al ángulo interno menor. Esta propiedad depende del tipo de triángulo, ya que existe una clasificación de triángulos que tiene todos sus lados de iguales.

Elementos

De los elementos de un triángulo, ya se mencionaron tres elementos básicos, los cuales son: vértice, lado y ángulo interno.

Además de estos, pueden distinguirse otros elementos que son muy importantes desde la geometría para el estudio de los triángulos.

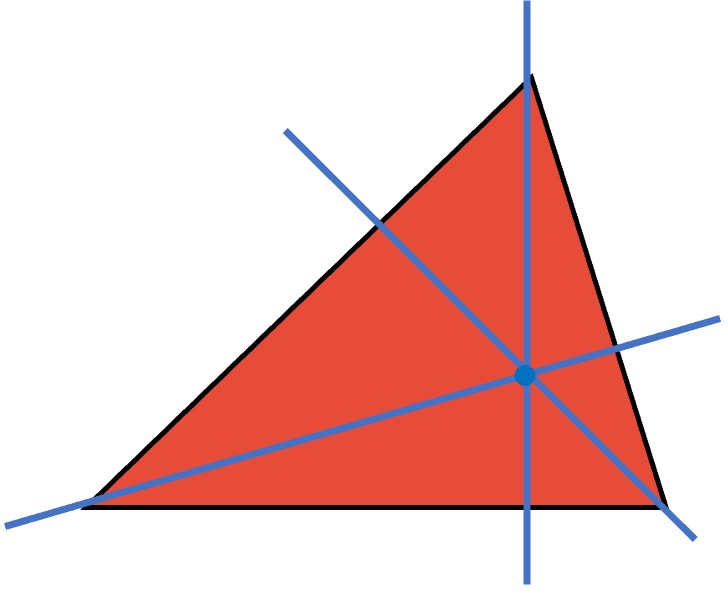
Altura

El segmento de recta perpendicular que se traza desde un vértice hasta su lado opuesto, se denomina altura del triángulo.

En el punto conocido como “ortocentro”, se cortan las tres alturas que se trazan en el triángulo.

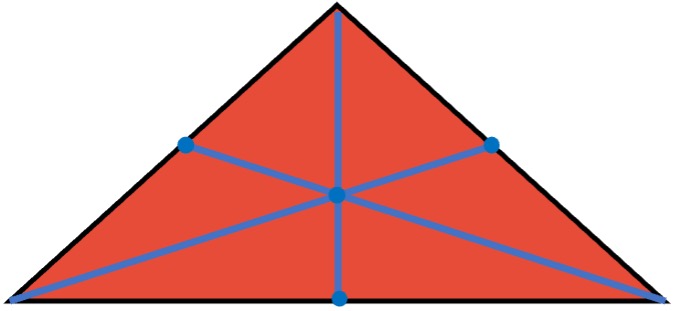
Mediana

• Artículo principal: Mediana de un triángulo.

Es la recta que se traza desde el punto medio de uno de los lados hasta su vértice opuesto.

El punto donde se cortan las medianas trazadas se llama “baricentro” o “centro de gravedad” del triángulo.

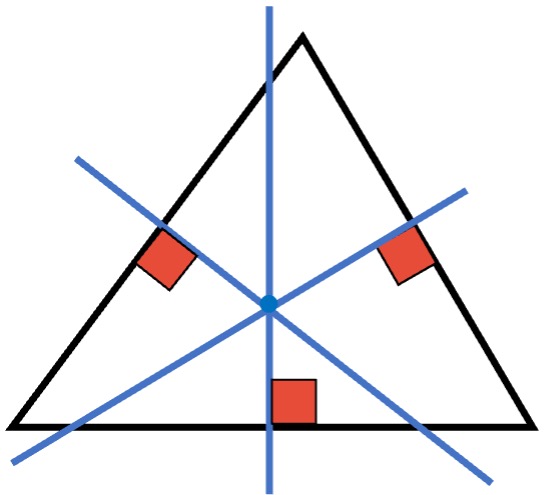
Mediatriz

Es la perpendicular trazada a un lado del triángulo y que pasa por el punto medio de dicho lado.

En el punto denominado como “circuncentro”, se cortan las mediatrices trazadas.

Bisectriz

• Artículo principal: Bisectriz.

Se denomina de esta manera al segmento de recta que divide por la mitad un ángulo del triángulo.

Las tres bisectrices que se trazan, se cortan en el punto denominado como “incentro”.

Tipos

La longitud de los lados y la amplitud de los ángulos, permiten clasificar los triángulos en dos categorías.

Según la longitud de sus lados

Según la longitud de sus lados, los triángulos se pueden clasificar en:

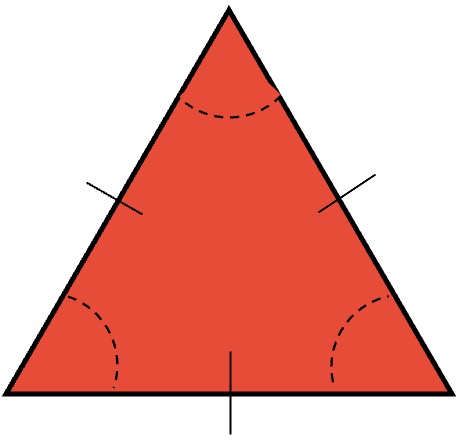
• Triángulo equilátero: es aquel que tiene sus tres lados de igual longitud y sus tres ángulos de igual amplitud, cada uno mide 60°.
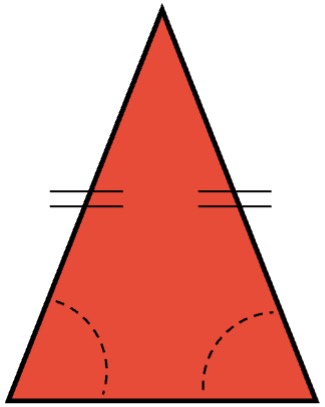
• Triángulo isósceles: este tipo de triángulo tiene dos lados de igual longitud y los ángulos opuestos a los lados iguales son de igual amplitud cada uno.
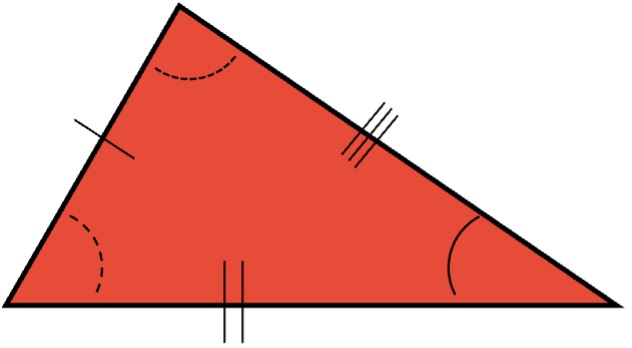
• Triángulo escaleno: es un tipo de triángulo que tiene sus tres lados de diferente longitud y los tres ángulos de diferente amplitud.

Según la amplitud o medida de sus ángulos

Según la amplitud o medida de sus ángulos se pueden clasificar en:

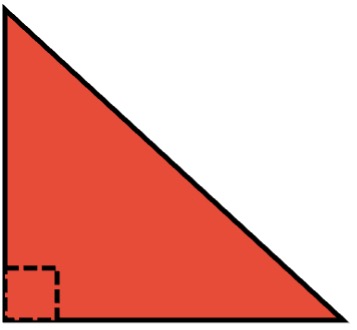
• Triángulo rectángulo: se denomina así, ya que tiene un ángulo igual a 90° al que se le conoce como ángulo recto. El lado opuesto al ángulo recto se conoce como hipotenusa.
• Triángulo acutángulo: es un triángulo con tres ángulos agudos, es decir cada uno de los ángulos tiene una amplitud menor a 90°.
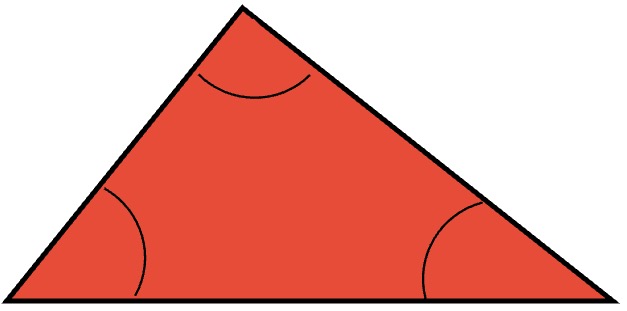
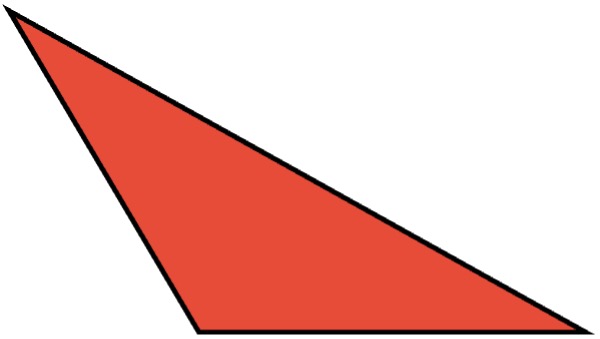
• Triángulo obtusángulo: este tipo de triángulo tiene un ángulo obtuso, es decir; tiene un ángulo con una amplitud mayor de 90°.

Perímetro y área

Todas las figuras geométricas bidimensionales tienen dos medidas básicas y fundamentales, estas son el perímetro y el área.

Perímetro

El perímetro de un triángulo se halla sumando las longitudes de cada uno de sus lados. Si se tiene un triángulo cuyos lados son: a, b, c, entonces:

Por ejemplo:la siguiente figura representa un triángulo cuyas medidas son: a = 2,4 cm., b = 2,8 cm. y c = 3,6 cm. El perímetro se calcularía de la manera siguiente:

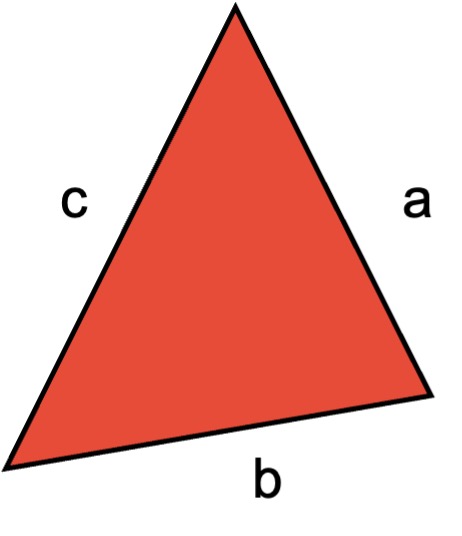
P = a + b + c, sustituyendo los valores en la fórmula quedaría: . El valor del Perímetro es: P = 8,8 cm.

Área

• Artículo principal: Área de un triángulo.

El área de un triángulo viene dada por la fórmula:

Dónde:

• A es el área
• b es la medida de la base del triángulo
• h es la altura del triángulo

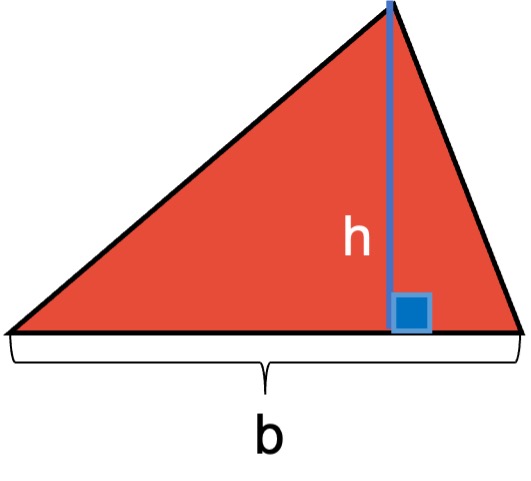
Por ejemplo, supóngase, un triángulo cuya base tiene una longitud de 18 cm y una altura de 8 cm., entonces aplicando la fórmula su altura sería:

Ejercicios resueltos

Ejercicio #1

Problema a resolver: dado el siguiente triángulo, indicar a qué tipo pertenece según la clasificación. a = 3,5 cm; c = 3 cm; d = 2,5 cm.

Ejercicio #2

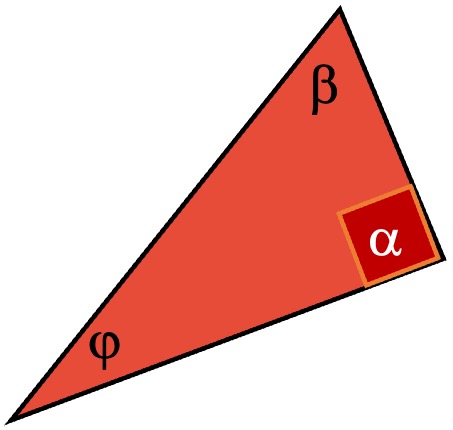
Problema a resolver: la figura muestra un triángulo cuyos ángulos miden: j = 40°, a = 90°. Calcular el valor de «b» e indicar qué tipo de triángulo es.

Ejercicio #3

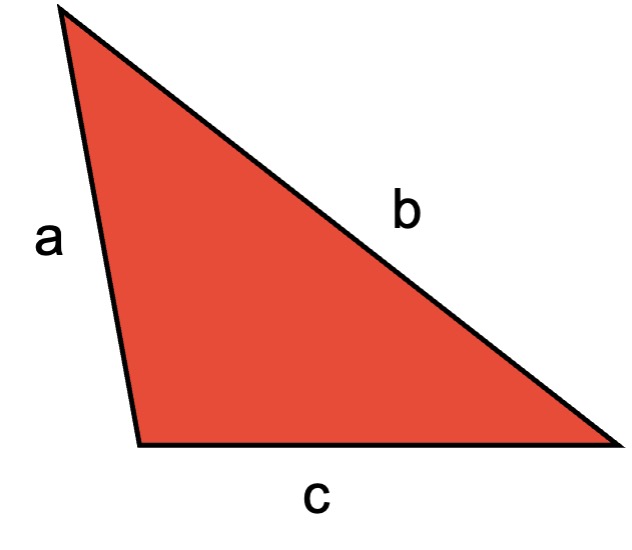
Problema a resolver: se tiene un triángulo cuyo perímetro es igual a 657 milímetros, si se conoce que dos de sus lados miden a = 200 milímetros y  b = 264 milímetros. Calcular el lado restante c.