Contenidos

Inicio / Matemática / Álgebra / Números enteros

Matemática

Álgebra

Números enteros

Conjunto de números que involucra a los números naturales y sus opuestos.

Por

Haude Medina

Tabla de contenidos:

Definición

El conjunto de los números enteros se denotan con la letra $\mathbb{Z}$ . A este conjunto pertenecen los números naturales y sus opuestos, es decir; los números positivos y negativos de la recta real, incluyendo el 0.

Para el caso, $\mathbb{Z}=\ \mathbb{Z}^-\cup{\ \mathbb{Z}}^+\cup\left\{0\right\}$ , expresado $\mathbb{Z}=(\ldots,\ -4,\ -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3,\ 4,\ \ldots,)$ . Los números negativos van precedidos del signo menos (-) y los positivos del signo positivo (+), aunque si este no se escribe se entiende que el número es positivo.

La siguiente figura muestra los números enteros en la recta numérica.

Conjunto de números enteros en recta númerica.

Los números negativos se ubican a la izquierda del cero y los positivos a la derecha del cero.

Los números enteros son los que se utilizan para contar, permiten diferenciar los saldos bancarios entre saldos negativos y positivos, deudas y haberes. Indicar temperaturas bajo cero o sobre cero, entre otros.

Propiedades

Con los números enteros se pueden realizar las operaciones básicas de la matemática como suma, resta, multiplicación y división. Para estas se cumplen ciertas propiedades que se listan a continuación:

Publicidad, continua debajo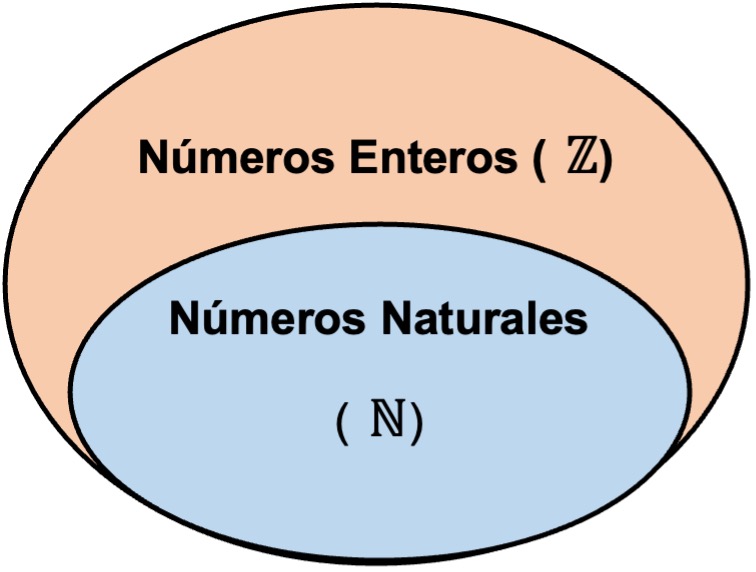

Conjunto de números enteros.

Propiedad interna: indica que al realizar cualquier operación de suma o multiplicación con números enteros, se obtendrá como resultado otro número entero. Se tiene que en la suma $a+b=c$ , donde $a,b,c\ \in\mathbb{Z}$ . Por ejemplo; -5 + 4 = -1, donde $(-1)\ \in\mathbb{Z}$ . En la multiplicación $a\ast b=c$ , donde $a,b,c\ \in\mathbb{Z}$ . Expresado con números se tiene, 6 * 3 = 18, donde $18\ \in\mathbb{Z}$ .
Propiedad conmutativa: refiere que el orden en el cual se encuentren los sumandos en una suma o los factores de una multiplicación, no altera el resultado. Para la suma se cumple que a+b=b+a. En cuanto a la multiplicación $a\ast b=b\ast a$ . A manera de ejemplo; en el caso de la suma: $100+\left(-53\right)=\left(-53\right)+100$ es igual a $47=47$ . Para el caso de la multiplicación $(-8)\ast3=3\ast(-8)$ es igual a $-24=-24$ .
Propiedad asociativa: esta propiedad refiere que la forma en que se agrupen los números enteros en la suma no afecta el resultado. $a+\left(b+c\right)=\left(a+b\right)+c$ . Por ejemplo $30+\left(5-20\right)=\left(30+5\right)-20$ . En el caso de la multiplicación la propiedad asociativa se expresa como: a * (b * c) = (a * b) * c. Utilizando números sería: $-2\ast\left(3\ast6\right)=\left(-2\ast3\right)\ast6$ .
Elemento neutro: para la suma el elemento neutro es el cero (0). A todo número entero que se le sume 0, el resultado es el mismo número entero. $55+0=55\$ . En cambio, en el caso de la multiplicación el elemento neutro es el 1, por lo que $a\ast1=a$ . Por ejemplo: $23\ast1=23,$ , $(-15)\ \ast\ 1\ =\ -15$ .
Elemento opuesto: refiere que si a cualquier número entero se le suma su número opuesto, esto da como resultado cero (0). Se expresa como $a + (-a) = 0$ . Por ejemplo $25 + (-25) = 0$ .

Operaciones

Suma de números enteros

Para la suma de números enteros se debe conocer la regla de los signos, la cual refiere que si los números tienen igual signo se suman los valores absolutos y se coloca el mismo signo en común.

En el caso de tener enteros con diferentes signos, se restan los valores absolutos de los sumandos y se escribe el signo del número cuyo valor absoluto sea mayor.

Suma de dos números enteros positivos: $(+9) + (+11) = +20$ .
Suma de dos números enteros negativos: $(-9) + (-11) = -20$ .
Suma de un número entero positivo y otro negativo: $(+9) + (-11) = -2$ .

Resta de números enteros

Si a y b son dos números enteros, entonces la sustracción entre a y b se expresada como $a -b$ , que es equivalente a: $a + (-b)$ .

La resta de $20\ -43$ , se puede efectuar como se indica a continuación:

$20 + (-43) = -23$ . Esto significa, que la sustracción de números enteros se puede expresar como una suma de enteros, según los casos mencionados en la adición de enteros.

Multiplicación de números enteros

Para este tipo de operación matemática se debe considerar la regla de los signos para la multiplicación, que indicará, una vez realizada la multiplicación, el signo que toma el producto o resultado.

Esta regla es la siguiente:

$+\ \ast\ +\ =\ +\ \rightarrow\ \ 8\ \ast\ 12\ =\ +96$

$+\ \ast\ -\ =\ -\ \rightarrow\ 8\ \ast\ (-12)\ =\ -96$

$-\ \ast\ +\ =\ -\ \rightarrow\ (-8)\ \ast\ 12\ =\ -96$

$-\ \ast\ -\ =\ +\ \rightarrow\ (-8)\ \ast\ (-12)\ =\ +96$

División de números enteros

La división exacta de dos números enteros consiste en hallar como resultado otro número entero. Para la división los elementos son:

$a\ \div b=c\$

donde «a» es el dividendo, «b» el divisor, debe ser diferente de (0) y «c» el cociente exacto.

Para divisiones inexactas el cociente no pertenecería al conjunto de los enteros.

Al igual que en la multiplicación, para determinar qué signo toma el resultado cuando se dividen enteros de diferentes signos, se debe aplicar la regla de los signos para la división.

$+\ \div\ +\ =\ +\ \ \ \rightarrow\ 12\ \ast\ 4\ =\ +3$

$+\ \div\ -\ =\ -\ \ \ \ \rightarrow\ 12\ \ast\ (-4)\ =\ -3$

$-\ \div\ +\ =\ -\ \ \ \rightarrow\ (-12)\ \ast\ 4\ =\ -3$

$-\ \div\ -\ =\ +\ \ \ \rightarrow\ (-12)\ \ast\ (-4)\ =\ +3$

Ejemplos

Algunos ejemplos de números enteros son:

4	8	-63	0
2	76	115	-53
65	34	12	23
6	15	25	93
1132	676	9348	100000

Ejercicios resueltos

Ejercicio #1

Problema a resolver: indique si ∈ o ∉ según corresponda:

-25		$\mathbb{Z}^-$
-37		$\mathbb{Z}^+$
123		$\mathbb{Z}^+$
18		$\mathbb{Z}^-$

Ver solución

Tabla de resultados:

-25	∈	$\mathbb{Z}^-$
-37	∉	$\mathbb{Z}^+$
123	∈	$\mathbb{Z}^+$
18	∉	$\mathbb{Z}^-$

Ejercicio #2

Problema a resolver: Realizar las siguientes operaciones:

$-20\ -\ (-46)\$
$-17\ +\ (-26)\$
$15\ +\ (-53)$
$-7\ \ast\ (-9)\$

Ver solución

Punto a)

Problema a resolver: $-20\ -\ (-46)\$

Solución: para eliminar el paréntesis se aplica ley de signos, – * – = +, entonces queda:

$-20\ +\ 46\ =\ 26$

Punto b)

Problema a resolver: $-17\ +\ (-26)\$

Solución: se suman los valores absolutos y se coloca el signo común:

$-17\ -\ 26\ =\ -\ 43$

Punto c)

Problema a resolver: $15\ +\ (-53)$

Solución: Se elimina el paréntesis por regla de signos, se restan los valores absolutos y se escribe el signo (-):

$15\ +\ (-53)\ =\ 15\ -\ 53\ =\ -38$

Punto d)

Problema a resolver: $-7\ \ast\ (-9)\$

Solución: se multiplican los números y los signos – * – = +:

$-7\ \bullet\ (-9)\ =\ +63$

Bibliografía:
Matemáticas para 1.er curso de ESO. (2016). Santillana. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Números enteros. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/numeros-enteros/). Última edición: mayo 2024. Consultado el 15 de octubre de 2024.

Copiar cita

¡Cita copiada a portapapeles!