Contenidos
Números negativos
Números menores que el cero (0).
Definición
Los números negativos son aquellos menores que el cero (0), por lo tanto, son menor que cualquier número positivo.
En la recta numérica se ubican a la izquierda del 0, por lo que cada número negativo representa el inverso aditivo de un número positivo.

Por ejemplo, el número -5 es el inverso aditivo del número +5 y se observa que ambos están a la misma distancia del 0 pero en lados opuestos.
Para distinguir los números negativos siempre se les antepone el signo negativo (-) y pueden ser números enteros como -3, -11, -52, también pueden ser fracciones
o decimales -7,8.
Entonces, los números negativos se leen como menos tres (-3), menos cincuenta y dos (-52), menos quince octavos .
Propiedades
Entre las propiedades que poseen los números positivos se pueden mencionar:
Publicidad, continua debajo- Se pueden definir como el conjunto de números reales menores a 0,
.
- En la recta numérica se ubican a la izquierda del 0.
- Al comparar dos números negativos, el de menor valor es el que se encuentra más alejado del 0, así, por ejemplo, -6 es menor que -2.
- Al comparar dos números de distinto signo, el número negativo siempre es menor al positivo.
- Al realizar operaciones aritméticas básicas con números negativos o positivos se debe considerar el signo, ya que este afecta el resultado.
- El valor absoluto de un número negativo, es el mismo número, pero sin el signo negativo. Por ejemplo; el valor absoluto de -13 es:
.
Operaciones
Los números negativos se pueden sumar, restar, multiplicar y dividir o se pueden desarrollar potencias, ya sea con base o exponente negativo, pero siguiendo ciertos criterios.
De manera general, para realizar las operaciones aritméticas se realizan los cálculos de los valores absolutos y por separado se determina el signo del resultado y en ocasiones se utilizan paréntesis para facilitar los cálculos.
Suma o resta de números negativos
Al sumar dos números negativos, se suman los valores absolutos y se escribe el signo negativo. El resultado siempre será otro número negativo.
negativo + negativo = negativo
Al sumar un número positivo con un número negativo o viceversa, se halla la diferencia de los valores absolutos y se escribe el signo del sumando de mayor valor absoluto. Por lo tanto, el resultado será un número negativo si el sumando negativo posee mayor valor absoluto que el positivo. Por ejemplo; -12 + 4 = -8. Como el número negativo posee mayor valor absoluto que el positivo el resultado es negativo. Por el contrario 12 + (–4) = 8
La resta se define como la suma del opuesto, entonces el opuesto de un número “a” es “-a”. Entonces para restar un número a otro se debe sumar el número opuesto al que se resta. Por ejemplo; (-4) – (-3) = (-4) + 3 = -1.
Para la suma se pueden aplicar las propiedades conmutativa y asociativa.
Multiplicación de números negativos
Para la multiplicación con números negativos realiza el producto de los valores absolutos de los factores y se aplica la regla de los signos.
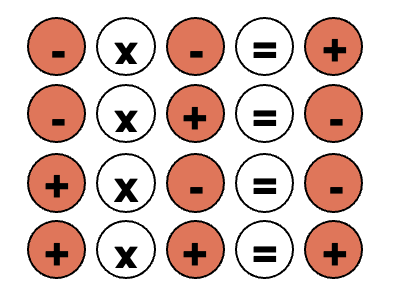
De esta manera, el resultado es un número negativo cuando se multiplican números de diferentes signos.
En esta operación aritmética se cumplen las propiedades conmutativa, asociativa y distributiva con respecto a la suma.
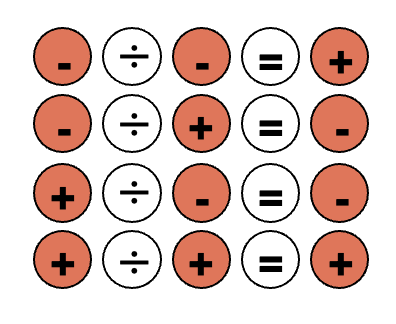
División de números negativos
Para el caso de la división se halla el cociente (resultado) de los valores absolutos de los números y se aplica la regla de los signos al igual que la multiplicación:
Potenciación con números negativos
Si un número negativo tiene un exponente par, el resultado siempre será un número positivo. Por ejemplo, (-5)2= (-5) * (-5) = 25.
Si un número negativo tiene un exponente impar, el resultado siempre será un número negativo. Por ejemplo, (-5)3= (-5) * (-5) * (-5) = -125.
Ejemplos
Ejemplos de números positivos de los diferentes conjuntos de números.
| -1963 | -638 | -15,5 | |
| -3,33 | -233 | -1 | |
| -2 | -772 | -25 | -32 |
Ejercicios resueltos
Ejercicio #1
Problema a resolver: para cada número negativo hallar el inverso aditivo.
- -6
- -231
- -1902
Ver solución
El inverso aditivo de un número negativo es el mismo número, pero con signo negativo, eso de resulta de multiplicar el negativo por -1, para cada caso se tiene:
- (-6) = -1(-6) = 6
- (-231) = -1(-231) = 231
- (-1902) = -1(-1902) = 1902
Ejercicio #2
Problema a resolver: ordenar de menor a mayor los siguientes números negativos.
| -76 | -4 | -23 | -54 | -19 | -20 |
Ver solución
Para los números negativos mientras más alejado del 0 se encuentre menor es su valor, también se puede decir que a mayor valor absoluto el número es menor. Ordenando se tiene:
| -76 | -54 | -23 | -20 | -19 | -4 |
Ejercicio #3
Hallar los resultados de las operaciones con números negativos.
- (-12)3
- (-3) + 8 – (-11)
- (-19) * (-10) * (-6)
Ver solución
- (-12)3 = (-12) * (-12) * (-12) = -1728
Por propiedad si la base es negativa y el exponente es impar, el resultado de la potencia será negativo. - (-3) + 8 – (-11) = -3 + 8 + 11 = -3 + 19 = 16
Al aplicar las propiedades estudiadas para la suma y resta se considera que el (-11) está restando por lo que pasa a una suma de su opuesto. Luego se suman los números de igual signo y el resultado se resta con el número de signo diferente. - (-19) * (-10) * (-6) = -1140
Para el producto de números negativos se multiplican los valores absolutos y luego se multiplican los signos.
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana