Contenidos
Expresiones algebraicas
Expresión compuesta por cifras numéricas con literales o bien solo letras.
Definición
Una expresión algebraica es una expresión compuesta por cifras numéricas con literales o bien solo letras, relacionadas por las operaciones básicas matemáticas de suma, resta, multiplicación y división, además de la potenciación y radicación.
No se debe confundir con una ecuación algebraica, ya que la expresión algebraica no representa una igualdad.
Expresiones del tipo 35t + 10t, 4 – 3x² – (5)², son expresiones algebraicas y se debe distinguir que los números y letras están conectados por signos de suma, resta potenciación, como se mencionó en la definición.
Aunque entre un número y una letra como en (35t), pareciera que no hay ninguna operación matemática, siempre existe una multiplicación y se debe tener en cuenta cuando se realicen operaciones con estas expresiones.
Las expresiones algebraicas son de gran utilidad para hallar el valor de cantidades desconocidas, áreas, distancias, entre otras.
Partes
Una expresión algebraica está compuesta por términos, que son los bloques o grupos de construcción de las expresiones y están formados por letras y números. Las letras o variables son el factor literal y los números o constante literal son llamados coeficientes.
Por ejemplo, 3x + 2y – 5, es una expresión algebraica que tiene 3 términos, 3x; 2y; – 5. La forma de escribir las expresiones algebraicas se conoce como notación algebraica.
Publicidad, continua debajoConocido esto, se mencionarán cada una los elementos de una expresión algebraica.
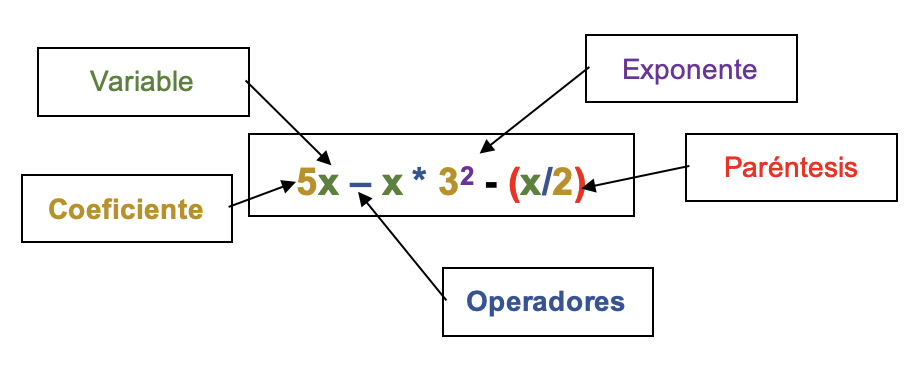
- Variable: es también llamada incógnita y es una letra que se utiliza para representar un número desconocido. Por lo general se utilizan las primeras letras del alfabeto (a, b, c, d, …) para cantidades conocidas y para las cantidades desconocidas las últimas letras como x, y, z.
- Coeficientes: son los números de los términos algebraicos y pueden tener signo positivo o negativo.
- Operadores: son los signos que indican que operación realizar, +, -, x, ÷. Se debe aclarar que para la multiplicación en las expresiones algebraicas se usa el punto (•) o el asterisco (*), debido a que el signo conocido de la multiplicación (x) puede confundirse con una variable. En el caso de la división en vez del signo ÷, se usa el signo (/), o se expresa como una fracción.
- Paréntesis: se usan para agrupar términos. En una expresión algebraica, como en cualquier operación aritmética, se deben resolver primero las expresiones que están dentro de ellos.
- Exponente: son potencias que indican que un número ha sido multiplicado por sí mismo varias veces.
Operaciones
Suma
La suma en expresiones algebraicas consiste en unir todos los términos en uno solo. Para realizar la suma de términos en una o más expresiones algebraicas estos deben ser semejantes. Si los términos no son semejantes se deja la suma expresada.
Los términos semejantes son aquellos que tienen el mismo factor literal e igual exponente (5x, 13x).
Entonces se suman los coeficientes de los términos semejantes considerando la regla de los signos. Por ejemplo, 9x2 + (-4x2) = 9x2 – 4x2 = 5 x2.
Resta
Esta operación matemática también responde a la regla de los signos y los términos deben ser semejantes. Si los términos no son semejantes se deja la suma expresada.
Si los dos números son positivos: se resta el sustraendo al minuendo. Si los dos números son negativos: se suman ambos números y se coloca signo negativo al resultado. Por ejemplo, 6y – 10y = -4y.
Multiplicación
Para expresiones algebraicas de un solo término, se multiplican los signos, luego los coeficientes entre sí, y se escriben las variables que sean iguales sumando los exponentes y las no semejantes.
Por ejemplo; 5xy2 + (-3x3) = 5xy2 – 3x3 = -15x(1+3)y2 = -15x4 y2.
En la multiplicación de una expresión algebraica de un solo término por una de varios términos, se aplica la propiedad distributiva.
División
Para la división se toma en cuenta la regla de los signos de la potenciación. Así, para expresiones algebraicas de un solo término se dividen los coeficientes, y luego las variables según la ley de exponentes (se restan los exponentes).
- División de un término entre otro,
.
- División de una expresión algebraica de varios términos entre un término algebraico. Para esto, primero se ordenan los términos de manera descendentes, luego se divide cada término de la expresión entre el término algebraico. Utilizando la propiedad distributiva. Por ejemplo;
.
- División de dos expresiones algebraicas de varios términos:
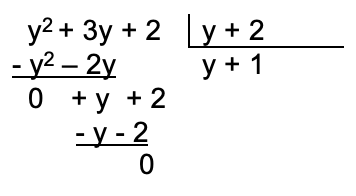
- Se ordenan los términos del divisor y el dividendo, según las potencias de la variable de forma descendente.
- Se halla el primer término del cociente, dividiendo el primer término del dividendo por el primer término del divisor.
- Se multiplica el cociente que se halló en el paso anterior, por todo el divisor y se ubican los productos debajo de los respectivos términos del dividendo.
- Se restan las cantidades.
Tipos
Las expresiones algebraicas se clasifican en:
- Monomio: son aquellas expresiones algebraicas que tienen un solo término. Por ejemplo, 4xy²; 5m; -12z⁵.
- Binomio: es una expresión algebraica con dos términos diferentes. Por ejemplo; -y³ + 9; 7m²n³ + 6m. Ciertamente un binomio es un polinomio.
- Polinomio: es una expresión algebraica que tiene más de un término algebraico diferentes o varios monomios distintos. Por ejemplo; 7y – 11xy – 3x.
Ejemplos
Algunos ejemplos de expresiones algebraicas son:
| 7y3 + 3x2 – 8 | X2 + 4 | 8xy² | -y3 – 2 |
| 4x + 13y – 7z | x2 – 2x + 15 | 4x2 + 8 | 3y + 25xy – 6x |
| -10z⁵ | X2 – 4 | 3y + 22 + y2 | 8x |
Ejercicios resueltos
Ejercicio #1
Problema a resolver: dado el polinomio 7y4 – 3y3 + y2 – 8, indicar lo siguiente.
- El coeficiente del segundo término.
- El coeficiente del tercer término.
- El exponente de la variable en el primer y tercer término.
- El término independiente.
Ver solución
El polinomio 7y4 – 3y3 + y2 – 8, tiene 4 términos para dar respuesta a cada pregunta se tiene:
- El coeficiente del segundo término es -3.
- El coeficiente del tercer término es 1.
- El exponente de la variable del primer término 4 y el exponente del tercer término es 2.
- El término independiente es -8.
Ejercicio #2
Problema a resolver: reducir el siguiente polinomio 3x – 8y +5x + 4z + 2x – 11y – 2z
Ver solución
Para reducir el polinomio, se hace la suma algebraica de los términos semejantes.
Los semejantes son:
3x – 8y + 5x + 4z + 2x – 11y – 2z
3x + 5x + 2x – 8y – 11y + 4z – 2z
10x – 19y + 2z
Ejercicio #3
Problema a resolver: realizar la multiplicación de los polinomios (x + 3) * (2x2 – 5x + 7).
Ver solución
Para realizar la multiplicación de los polinomios dados se debe multiplicar los términos del primer polinomio por cada uno de los términos del segundo polinomio.
(x + 3) * (2x2 – 5x + 7)
X*2x2 – x*5x + 7*x + 3*2x2 – 3*5x + 3*7
2x3 – 5x2 + 7x + 6x2 – 15x + 21
(se suman o restan los términos semejantes)
2x2 + x2 – 8x + 21
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana