Contenidos

Inicio / Historia y Sociedad / Cilindro

Matemática

Geometría

Cilindro

Cuerpo geométrico sólido cuyos extremos o bases son circulares y tiene una cara curva.

Por

Haude Medina

Tabla de contenidos:

Definición

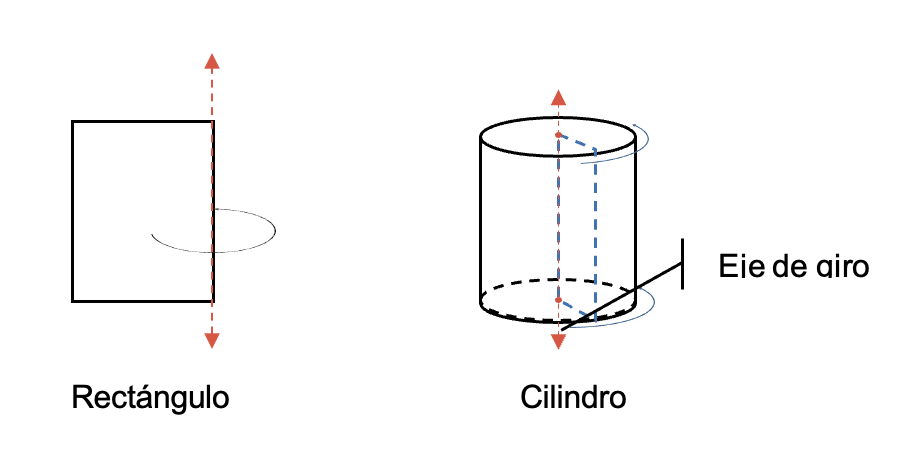
Un cilindro es un cuerpo geométrico sólido cuyos extremos o bases son circulares y tiene una cara curva, que se forma cuando se hace girar un rectángulo tomando como eje uno de sus extremos.

También se define como una superficie formada por rectas paralelas, cada una de las cuales contiene un punto de una curva plana llamada directriz del cilindro.

El cilindro se clasifica como un cuerpo redondo dentro de las figuras geométricas tridimensionales por tener al menos una cara curva. Este tipo de figura tiene tres dimensiones, largo, ancho y alto, es decir tienen volumen y ocupan un lugar en el espacio.

En la figura, se puede observar el rectángulo que se hace girar sobre su base para formar la cara del cilindro

Rectángulo y cilindro, referencias.

Características

Entre las características a destacar de los cilindros se pueden mencionar las siguientes:

El cilindro es una figura tridimensional.
Es conocida como un cuerpo de revolución, ya que se origina al hacer girar una figura plana alrededor de un eje.
El cilindro tiene volumen y área superficial.
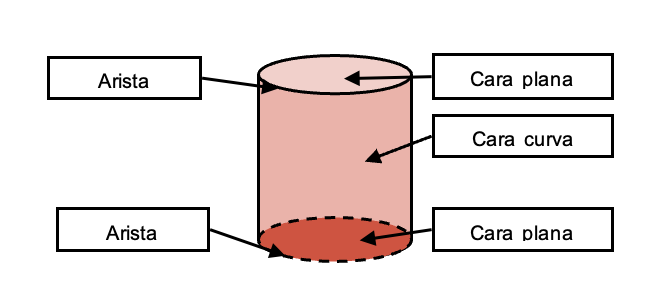
Un cilindro tiene 3 caras, dos son planas y otra curva. Además posee 2 aristas y no posee ningún vértice.
Las bases del cilindro pueden ser dos círculos o dos elipses. Dependiendo de estas, se puede clasificar el cilindro en circular o elíptico.
Las bases inferior y superior son congruentes y paralelas entre sí.
Un cilindro es semejante a un prisma, por tener la misma sección transversal en todas partes.

Partes

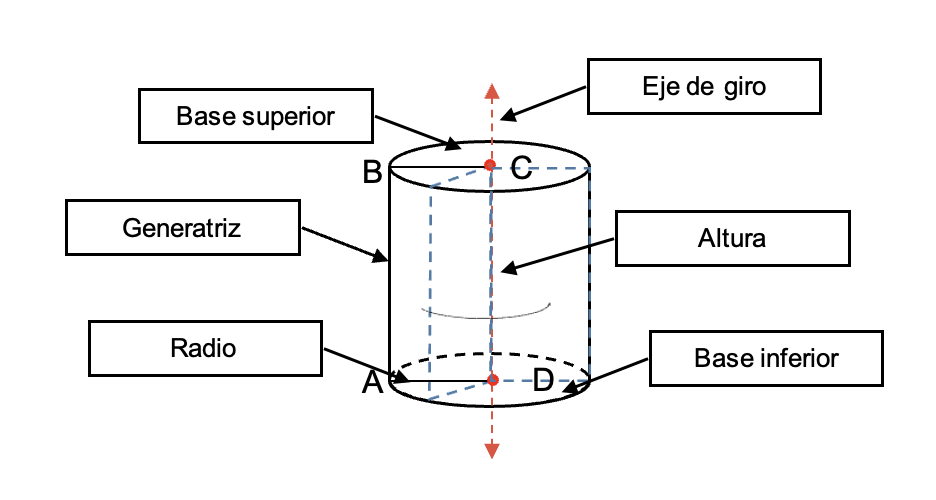
En un cilindro se distinguen los siguientes elementos:

Publicidad, continua debajo

Base: son los círculos que generan los lados $\overline{AD}$ y $\overline{BC}$ . Son dos bases, una superior y otra inferior.
Radio (r): es la distancia que existe entre el centro del cilindro y el extremo. En la figura los lados $\overline{AD}$ y $\overline{BC}$ son los radios.
Altura (h): es la distancia del segmento que se traza de forma perpendicular uniendo las bases. En la figura el segmento $\overline{CD}$ correspondería a la altura.
Eje de giro: es la recta imaginaria sobre la cual se gira el rectángulo para generar el cilindro.
Generatriz (g): corresponde al lado opuesto al eje del cilindro. El lado $\overline{AB}$ es la generatriz y coincide con la medida de $\overline{CD}$ que es la altura.

Partes de un cilindro.

Tipos

Los cilindros se pueden clasificar según el ángulo de inclinación de la generatriz con respectos a sus bases y según la forma de sus bases, si es un círculo o una elipse.

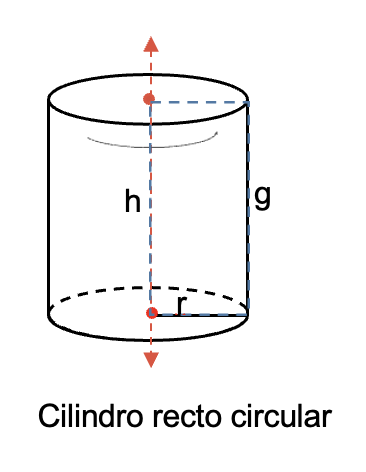
Cilindro recto circular: tienen la particularidad de que sus bases son circulares y se denomina recto, debido a que la generatriz es perpendicular al plano de la base y tiene la misma medida de la altura.
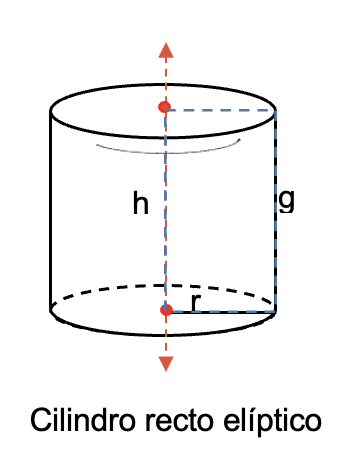
Cilindro recto elíptico: para este tipo sus bases son dos elipses y al igual que el cilindro recto circular, el eje de rotación es perpendicular a las bases.
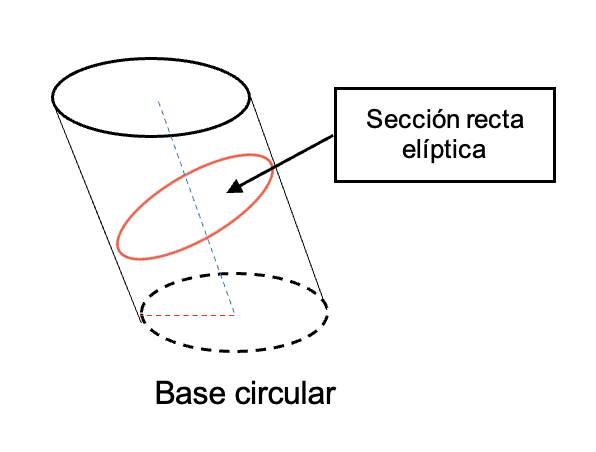
Cilindro oblicuo circular: en este tipo de cilindro, la generatriz (altura) es oblicua al plano de la base que son circulares y la sección recta al eje es una elipse.
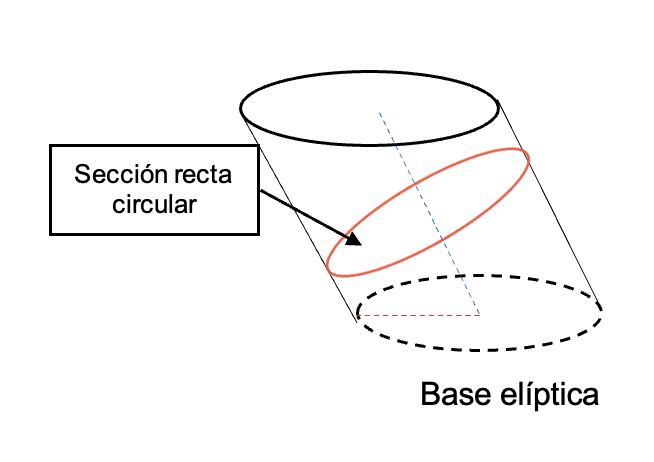
Cilindro oblicuo elíptico: el ángulo que se forma entre el eje y las bases no es perpendicular. Para este tipo de cilindro, las bases son elipses y la sección recta al eje es un círculo.

Perímetro y área

Perímetro

En un cilindro, por lo general, se calcula el perímetro de la base inferior, esto permite conocer qué porción del plano ocupa la figura geométrica.

De esta manera el perímetro de la base inferior se calcula mediante la fórmula:

$P=2\ast\pi\ast r$

Área

El área total de un cilindro recto, viene dada por la suma del área lateral y el área de la base inferior y la base superior.

Según la definición del área total del cilindro, expresado como fórmula matemática se hallaría de la siguiente manera:

$A_t=A_l+2A_b$

El área de la base, viene dada en función del radio, y se hace calcula a través de la fórmula:

$A_b=\pi\ast r^2$

El área lateral se calcula en función de la altura y el radio del cilindro y la fórmula es:

$A_l=2\ast\pi\ast r\ast h$

Sustituyendo $A_b$ y $\ A_l$ , en la fórmula del área total se tiene que:

$A_t=\left(2\ast\pi\ast r\ast h\right)+2\left(\pi\ast r^2\right)$

$A_t=2\pi r(h+r)$

Ejercicios resueltos

Ejercicio #1

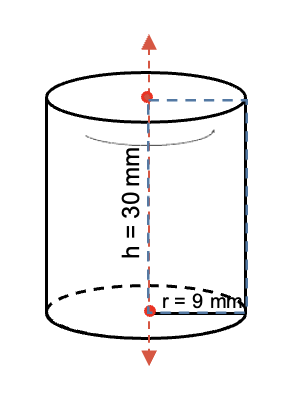
Problema a resolver: en el cilindro que se muestra en la figura, la medida de la altura es de 30 mm. y el radio de la base es de 9mm. ¿Calcular el área total?

Ejercicio de cilindro.

Ver solución

Utilizando la fórmula conocida del área total, donde $A_t=2\pi r(h+r)$ , se sustituyen los valores dados, recordando que el valor de $\pi=3,1416$ .

$A_t=2\left(3,1416\right)\left(9\right)\left(30+9\right)$

$A_t=54,55\ast39=2205,40\ {mm}^2$

El área total del cilindro es de 2205, 40 mm².

Ejercicio #2

Problema a resolver: para el ejemplo anterior, calcular el perímetro de la base.

Ver solución

El perímetro de la base del cilindro se halla utilizando la fórmula:

$P=2\ast\pi\ast r\$

sustituyendo los valores se tiene:

$P=2\ast\left(3,1416\right)\ast\left(9\right)=56,55\ mm\$

El perímetro de la base inferior es de 56,55 mm.

Ejercicio #3

Problema a resolver: se tiene un cilindro, cuyo perímetro de la base es de 43 cm. y la altura 15 cm. Calcular el área del cilindro.

Ver solución

Como se tiene el perímetro de la base se puede hallar el valor del radio (r).

$P=2\ast\pi\ast r$

despejando el radio de la fórmula se obtiene que

$r=\frac{P}{2\pi}=\frac{43}{2\left(3,1416\right)}=\frac{43}{6,28}$

$r=6,8\ cm$

Obtenido el valor del radio que es 6,8 cm, se puede hallar el área total del cilindro.

$A_t=2\pi r(h+r)$

$A_t=2\left(3,1416\right)\left(6,8\right)\left(15+6,8\right)$

$A_t=42,73\ast21,8=931,4\ {cm}^2$

El área del cilindro es de 931,4 cm²

Bibliografía:
Ministerio de Educación del Ecuador. (2016). Matemática 9° grado. Libro del estudiante. SMEcuaediciones. Ministerio de Educación del Ecuador. (2016b). Matemática 10° grado. Libro del estudiante. SMEcuaediciones.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Cilindro. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/cilindro/). Última edición: mayo 2022. Consultado el 18 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!