Enciclopedia Iberoamericana
Contenidos
Formas indeterminadas
Situaciones matemáticas en las que una expresión o una operación aritmética no tiene un valor definido o único, siendo imprecisos.
Definición
Las indeterminaciones en matemáticas son situaciones en las que una expresión o una operación aritmética no tiene un valor definido o único, siendo imprecisos.
En el cálculo de límites, una indeterminación se presenta en situaciones en las que, al evaluar el límite de una función, se obtiene un resultado que no puede determinarse de manera directa.
La función asume una forma especial como como 
Es importante recordar que obtener una indeterminación al calcular un límite no significa que el límite no exista.
En estos casos, es necesario utilizar técnicas especiales para resolver la indeterminación y obtener el valor del límite.
Tipos
En el cálculo de límites, existen diferentes tipos de indeterminaciones, cada una con sus características y métodos de resolución.
A continuación, se presenta una descripción de las indeterminaciones más comunes.
Publicidad, continua debajo
Indeterminación del tipo 0/0
Se produce cuando tanto el numerador como el denominador tienden a cero simultáneamente.
Por ejemplo, al evaluar el límite 
, cuando x tiende a 2, tanto el numerador como el denominador tienden a cero cuando. lo que resulta en una indeterminación de tipo 
Indeterminación del tipo ∞/∞
Ocurre cuando al evaluar el límite de una función, tanto el numerador como el denominador tienden a infinito o menos infinito (simultáneamente).
Por ejemplo, al calcular 
, tanto el numerador como el denominador crecen indefinidamente cuando x se acerca a infinito.
Indeterminación del tipo ∞ – ∞
Se presenta cuando la diferencia entre dos términos tiende a infinito o menos infinito.
Por ejemplo, al evaluar 
, la diferencia entre el término de la raíz y la x tienden a infinito, por lo que se obtiene una resta de ∞ – ∞, siendo una indeterminación.
Indeterminación del tipo 0*∞
Ocurre cuando se multiplica un término que tiende a cero por otro que tiende a infinito.
Indeterminación del tipo ∞⁰
Se presenta cuando una función toma la forma de elevado a la potencia de cero.
Indeterminación del tipo 0⁰
Ocurre cuando una función toma la forma de cero elevado a la potencia de cero. Por ejemplo, al evaluar 
, tanto la base como el exponente tienden a cero cuando se aproxima a cero.
Indeterminación del tipo 1^∞
Se presenta cuando una función toma la forma de uno (1) elevado a la potencia de infinito (∞).
Por ejemplo, al calcular 
, la base tiende a 1 y el exponente tiende a infinito cuando x se aproxima a infinito.
Métodos de resolución
Estas indeterminaciones son fundamentales en el análisis matemático y requieren técnicas específicas para su resolución, como el uso de límites, la factorización, la regla de L’Hôpital y otras herramientas avanzadas del cálculo.
Sin embargo, es importante comprender cómo y cuándo aplicar cada método según el contexto específico del problema.
Indeterminación 0/0
Este tipo de indeterminación que se obtiene al evaluar un límite, se puede resolver aplicando estrategias como:
- Factorización tanto de numerador como el denominador y luego simplificar la expresión, si es un cociente de polinomios.
- Multiplicando y dividiendo por el conjugado, en el caso de radicales.
- Regla de L’Hôpital
Indeterminación del tipo ∞/∞
En este caso, se puede intentar dividir tanto el numerador como el denominador por la potencia dominante de la variable.
Después de esta división, se evalúa el límite nuevamente para resolver.
En el caso de persistir su indeterminación de tipo , se recomienda aplicar la regla de L’Hôpital o utilizar otras técnicas de factorización para simplificar la expresión.
Indeterminación del tipo ∞ – ∞
Para resolver este tipo de indeterminaciones, se puede intentar agrupar términos semejantes y luego factorizar la expresión.
En el caso de radicales se resuelve multiplicando y dividiendo por el conjugado.
Indeterminación del tipo 0*∞
En estas situaciones, se intenta reescribir la expresión utilizando alguna identidad trigonométrica o manipulando los términos para convertir la indeterminación en una forma más manejable, como 0/0 o ¥/¥, y luego aplicar las técnicas correspondientes.
Indeterminación del tipo 1^∞
En estos casos, una estrategia efectiva es utilizar propiedades de los logaritmos para convertir la expresión en una forma que pueda ser tratada con otras técnicas, como las indeterminaciones de tipo 0/0 o ¥/¥.
Luego, se puede aplicar la regla de L’Hôpital o técnicas de factorización para resolver la indeterminación.
Indeterminación del tipo 0^∞
Para resolver estas indeterminaciones, por lo general se aplican logaritmos naturales u otras funciones para transformar la expresión en una forma más manejable.
Indeterminación del tipo 0⁰
En este caso, una estrategia común es utilizar las propiedades de los logaritmos o manipular algebraicamente la expresión para convertirla en una forma que pueda ser tratada con otras técnicas.
Luego, se puede aplicar la regla de L’Hôpital o sustituir funciones para resolver la indeterminación.
No indeterminantes
Existen caso en los cuales al evaluar el límite se obtienen resultados con cero (0) o infinitos (∞) que involucran un valor finito, como los siguientes:
Donde k es un valor finito.
Ejercicio resuelto
Evaluar el límite 
Ver solución
Al resolver el límite se obtiene:
Se obtiene una indeterminación del tipo
Para este caso, se puede aplicar el método de factorización 
Finalmente se logró resolver la indeterminación obteniendo que:
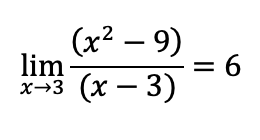
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.