Contenidos
Polígono
Figura plana cerrada, que se forma de la unión de varios segmentos de rectas, que solo se intersectan de dos en don en sus extremos
Definición
Un polígono es una figura geométrica plana cerrada, que se forma de la unión de varios segmentos de rectas, que solo se intersectan de dos en dos en sus extremos, es decir, que se unen dos segmentos de recta consecutivos en el punto llamado vértice.
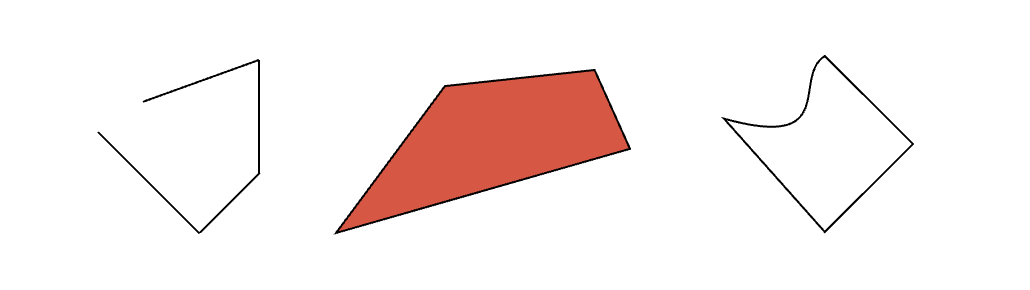
De las siguientes figuras, tan solo la segunda es un polígono, por ser una figura plana, tener líneas rectas que lo forman y es cerrada. En cambio la primera no cumple la condición de ser una figura cerrada y la tercera tiene líneas curvas, por tanto, no son polígonos.
Características
Como se ha mencionado, un polígono se caracteriza por ser una figura plana, ser cerrada y estar formada por segmentos de recta.
Además de estas tres características básicas, se pueden encontrar otras como las que se mencionan a continuación:
- Los polígonos tienen la misma cantidad de lados que de ángulos y de vértices.
- Para nombrar un polígono se emplean las letras que identifican sus vértices.
- Desde un vértice de un polígono se pueden trazar (n – 3) diagonales, donde “n” es el número de lados.
- La suma de los ángulos externos de cualquier polígono siempre es igual a 360°.
Tipos y clasificación
Los polígonos se pueden clasificar de diferentes maneras, la primera y más general de ellas es según la medida de ángulos y lados:
Según sus lados y ángulos
Es la más general ya que utiliza estos dos elementos del polígono para distinguir sus tipos:
Publicidad, continua debajo- Polígonos regulares: tienen todos sus lados congruentes y todos sus ángulos tienen la misma medida de amplitud.
- Polígonos irregulares: son aquellos que tienen al menos un lado o un ángulo desigual.

Según el número de lados del polígono
Para esta clasificación, se considera únicamente la cantidad de lados del polígono:
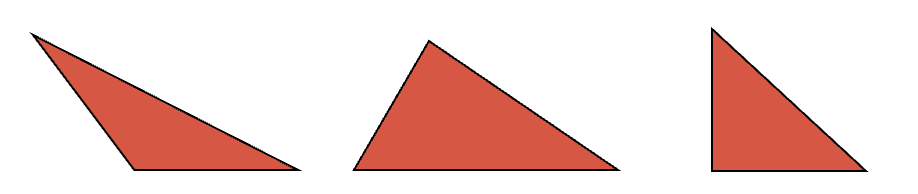
- Triángulos: que es una figura plana con 3 lados, 3 vértices y 3 ángulos, sus ángulos interiores suman 180°. Estos a su vez se pueden clasificar según la longitud de sus lados en: equilátero, isósceles y escaleno. Y según la medida de sus ángulos es rectángulo, acutángulo y obtusángulo.
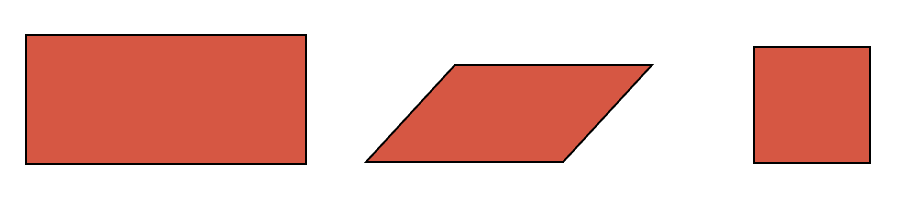
- Cuadriláteros: son otro tipo de polígonos que tienen 4 lados, 4 vértices y 4 ángulos internos. Estos a su vez se clasifican en Paralelogramo (tienen lados paralelos dos a dos) y No Paralelogramo (no tiene lados paralelos).
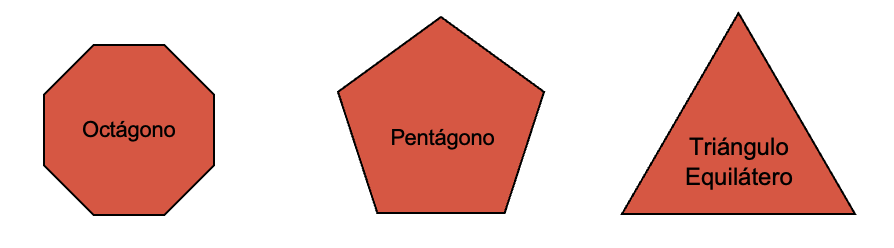
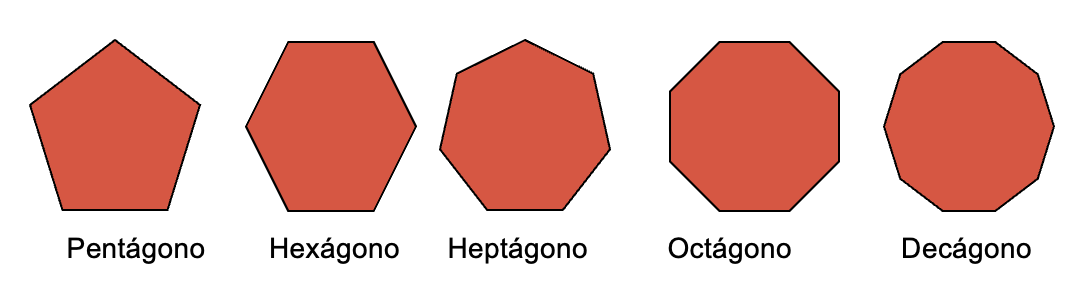
- Pentágono: tiene cinco lados.
- Hexágono: tiene seis lados.
- Heptágono: que es un polígono de siete lados.
- Octágono: el cual tiene ocho lados.
- Nonágono: que es el polígono de nueve lados
- Decágono: el cual tiene 10 lados.
Según los ángulos del polígono
Para esta clasificación se tiene en cuenta los ángulos interiores:
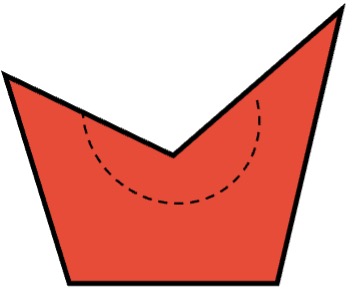
- Cóncavos: son aquellos polígonos en el que por lo menos uno de sus ángulos interiores mide más de 180°.
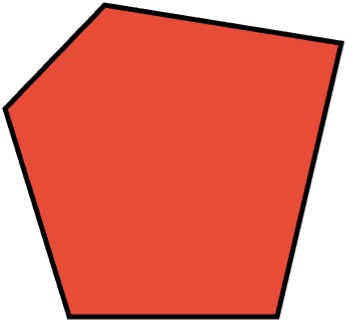
- Convexo: cumple con la característica de que todos sus ángulos interiores miden menos de 180°.
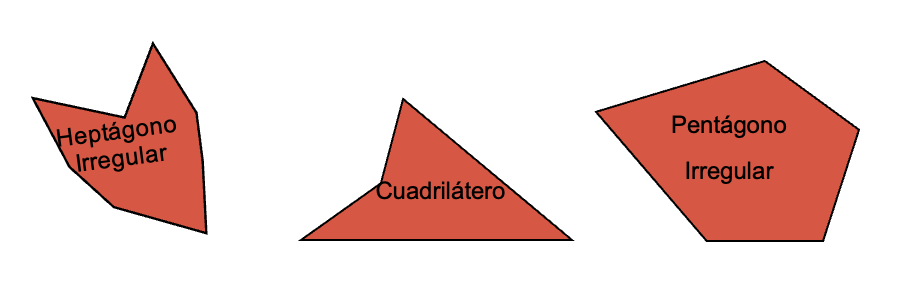
La clasificación de los polígonos regulares e irregulares se puede combinar con los tipos de polígonos según sus lados. Así, de esta manera, se puede tener las figuras vistas y de esta manera:
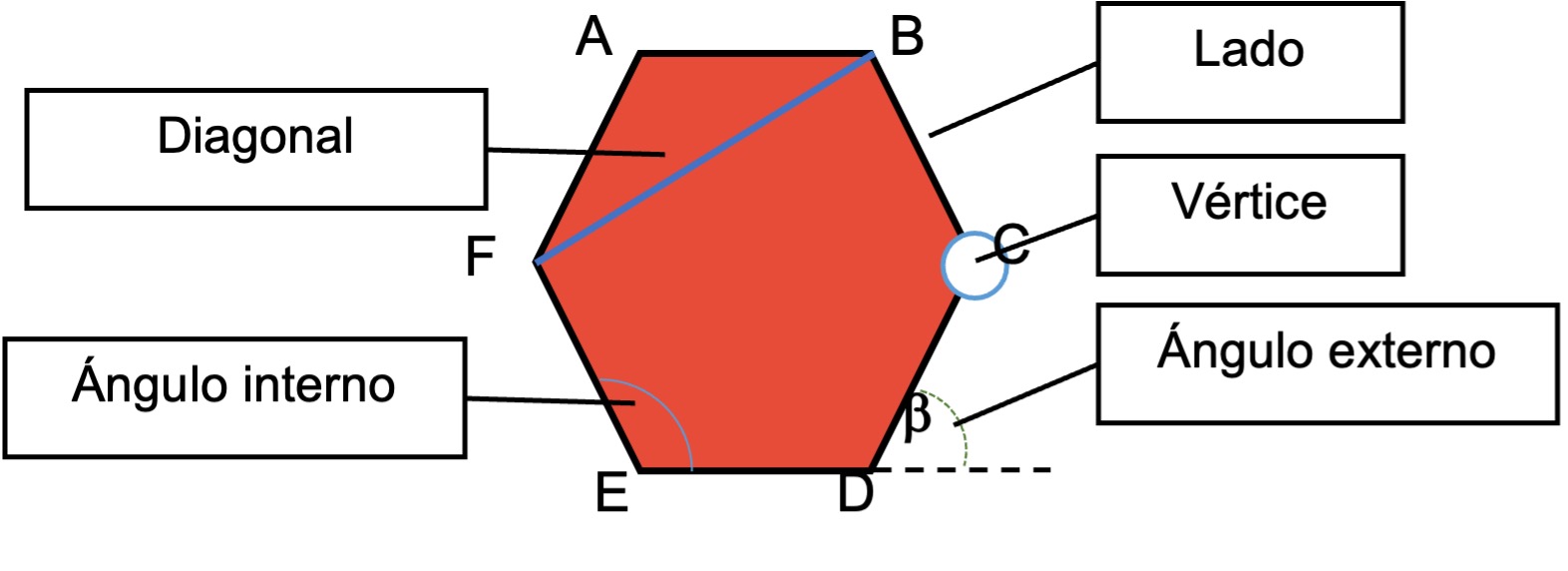
Elementos
Los polígonos constan de los siguientes elementos:
- Lados: son los segmentos de recta que forman el polígono. Se pueden nombrar según los vértices de sus extremos:
,
,
,
,
,
.
- Vértices: es el punto donde concurren dos lados o segmentos de recta. Se A, B, C, D, E, F.
- Ángulos interiores: son ángulos que están dentro del polígono y que se forma de la intersección de dos lados consecutivos.
,
,
,
,
,
. La suma de los ángulos internos de cualquier polígono depende de la cantidad de lados que este tenga y se halla mediante la fórmula: Suma de
= (n – 2) *180°, donde “n” es el número de lados del polígono.
- Ángulos externos: son los ángulos fuera del polígono. Son suplementarios a los internos.
- Diagonales (D): son segmentos de recta que unen dos vértices no consecutivos. La cantidad de diagonales de un polígono se calcula mediante la fórmula:
donde n representa el número de lados.
La siguiente figura representa cada uno de los elementos de un polígono:
Ejercicios resueltos
Ejercicio #1
Problema a resolver: complete la siguiente tabla indicando para los polígonos dados cuál es el valor de la suma de sus ángulos internos.
| Polígono | Lados | Fórmula | Suma ángulos internos |
| Triángulo | 3 | ||
| Cuadrilátero | 4 | ||
| Pentágono | 5 | ||
| Hexágono | 6 | ||
| Decágono | 10 |
Ver solución
| Polígono | Lados | Fórmula | Suma ángulos internos |
| Triángulo | 3 | Suma de Suma de |
180° |
| Cuadrilátero | 4 | Suma de Suma de |
360° |
| Pentágono | 5 | Suma de Suma de |
540° |
| Hexágono | 6 | Suma de Suma de |
720° |
| Decágono | 10 | Suma de Suma de |
1440° |
Ejercicio #2
Problema a resolver: para el siguiente cuadro complete la cantidad de diagonales de cada polígono.
| Polígono | Lados | Fórmula | Diagonales |
| Hexágono | 6 | ||
| Octágono | 8 | ||
| Cuadrilátero | 4 |
Ver solución
| Polígono | Lados | Fórmula | Diagonales |
| Hexágono | 6 | 9 | |
| Octágono | 8 | 20 | |
| Cuadrilátero | 4 | 2 |
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana