Contenidos

Inicio / Historia y Sociedad / Fracciones mixtas

Matemática

Álgebra

Fracciones mixtas

Aquella fracción compuesta de dos partes: por un número entero y por una fracción propia.

Por

Haude Medina

Tabla de contenidos:

Definición

Los números mixtos o fracciones mixtas son un tipo de fracción que se denominan de esta manera por estar compuesta de dos partes: por un número entero y por una fracción propia (se entiende por fracción propia, aquella cuyo numerador es menor al denominador).

Entonces, una fracción mixta es de la forma $a\frac{b}{c}$ donde $a$ representa el número entero y $\frac{b}{c}$ la fracción propia.

Un ejemplo de fracción mixta es $3\frac{1}{4}$ que se lee como «tres y un cuarto», donde el número $3$ es la parte entera y $\frac{1}{4}$ es la fracción propia.

Esta fracción de manera gráfica se representa de la siguiente manera:

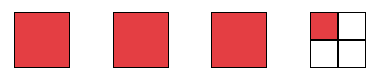
$Representación gráfica de las fracciones mixtas$

Lo que significa, que se toman 3 partes enteras y de la otra parte entera se toma tan solo un cuarto ¼ de ella. Por esta razón, también se puede definir una fracción mixta como la representación de un número que se obtiene al sumar el entero y la fracción propia $3$ + $\frac{1}{4}$ .

Una fracción del tipo $2\frac{4}{3}$ , no se considera como una fracción mixta, esto debido a que la parte fraccionaria es una fracción impropia, donde el numerador es mayor al denominador, lo que significa que existe más de una unidad completa.

Publicidad, continua debajo

Por el contrario, las fracciones impropias pueden expresarse en forma de fracciones mixtas y viceversa.

Fracciones mixtas a impropias

Con las fracciones mixtas se pueden realizar las operaciones matemáticas básicas, suma, resta, multiplicación y división. Sin embargo, para multiplicar o dividir con fracciones mixtas, previamente se deben convertir en fracciones impropias.

El proceso para convertir fracciones mixtas en fracciones impropias es el siguiente:

Paso 1: se iguala la fracción, colocando el denominador de la parte fraccionaria hacia el otro lado del signo de igualdad.
Paso 2: multiplicar el entero de la fracción mixta por el denominador de la parte fraccionaria.
Paso 3: sumar el resultado de la operación anterior con el numerador de la parte fraccionaria.
Paso 4: el resultado obtenido, se coloca como numerador al otro lado de la igualdad.

Se puede generalizar el procedimiento descrito a partir de la siguiente fórmula:

$a\frac{b}{c}=\frac{\left(a\ast c\right)+b}{c}$

Donde $a$ es el número entero, $b$ es el numerador de la fracción propia y $c$ es el denominador.

Para comprender mejor el proceso, se desarrolla el siguiente ejemplo: Convertir la fracción mixta $5\frac{1}{3}$ a fracción impropia. Aplicando la fórmula dada se obtiene:

$5\frac{1}{3}=\frac{\left(5\ast3\right)+1}{3}=\frac{16}{3}$

Por tanto, la fracción mixta $5\frac{1}{3}$ es igual a la fracción impropia $\frac{16}{3}$ .

Para entender el proceso de manera gráfica, se debe partir de que, cada unidad está dividida en 3 partes iguales, como indica el denominador.

Ahora bien, como el numerador son 16 partes, se debe continuar representando otras figuras idénticas a la anterior y, continuar con el conteo, hasta llegar a tomar 16 partes iguales.

Esta es la representación gráfica de la fracción mixta $5\frac{1}{3}$ , que tiene 5 partes enteras y 1/3.

$Representación gráfica de la fracción impropia a mixta$

Las fracciones mixtas, se pueden comprender más mejor de manera visual, si se tiene una representación gráfica, esta fácilmente se puede expresar en forma de fracción mixta o fracción impropia. Veamos otro ejemplo:

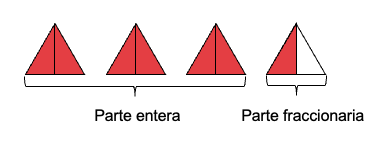
$Representación gráfica de las fracciones mixtas$

La gráfica, se puede expresar como una fracción mixta de la siguiente manera $3\frac{1}{2}$ , ya que se han tomado 3 partes enteras y la mitad de la otra unidad, es decir $\frac{1}{2}$ . Para representarla a manera de fracción impropia sería $\frac{7}{2}$ .

Ejemplo

Algunos ejemplos de fracciones mixtas son:

$5\frac{1}{5}$	$3\frac{2}{3}$	$7\frac{3}{9}$	$1\frac{9}{4}$
$12\frac{1}{3}$	$7\frac{23}{5}$	$6\frac{1}{2}$	$10\frac{17}{2}$
$2\frac{4}{8}$	$12\frac{64}{23}$	$8\frac{14}{9}$	$9\frac{1}{15}$

Ejercicios resueltos

Ejercicio #1

En el cuadro a continuación hay una serie de fracciones mixtas, indicar como se lee cada una de ellas.

Fracción mixta	Se lee…
$4\frac{3}{5}$	Cuatro enteros y tres quinto
$1\frac{4}{7}$	Un entero y cuatro séptimo
$6\frac{3}{10}$	Seis enteros y tres décimos
$3\frac{11}{100}$	Tres enteros y once centésimos
$23\frac{8}{13}$	Veintitrés enteros y ocho treceavos

Ejercicio #2

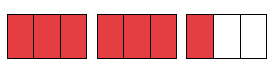
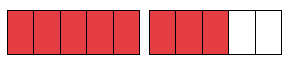
Indicar la fracción mixta y fracción propia de las siguientes representaciones gráficas.

Representación gráfica	Fracción mixta	Fracción impropia
$Imagen de ejemplo 1 de las fracciones mixtas$	$2\frac{1}{3}$	$\frac{7}{3}$
$Imagen de ejemplo 2 de las fracciones mixtas$	$1\frac{3}{5}$	$\frac{8}{5}$
$Imagen de ejemplo 3 de las fracciones mixtas$	$6\frac{4}{7}$	$\frac{46}{7}$

Ejercicio #3

Convertir las fracciones mixtas a fracciones impropias.

Punto A

Fracción a convertir: $2\frac{5}{8}$ .

Ver solución

Aplicando la fórmula $a\frac{b}{c}=\ \frac{\left(a\ast c\right)+b}{c}$ obtenemos el siguiente resultado:

$2\frac{5}{8}=\ \frac{\left(2\ast8\right)+5}{8}=\frac{21}{8}$

Por tanto, la fracción mixta $2\frac{5}{8}$ es igual a la fracción impropia $\frac{21}{8}$ .

Punto B

Fracción a convertir: $4\frac{1}{9}$ .

Ver solución

Aplicando la fórmula mencionada anteriormente se obtiene el siguiente resultado:

$4\frac{1}{9}=\ \frac{\left(4\ast9\right)+1}{9}=\frac{37}{9}$

Por tanto, la fracción mixta $4\frac{1}{9}$ es igual a la fracción impropia $\frac{37}{9}$ .

Punto C

Fracción a convertir: $-3\frac{7}{11}$ .

Ver solución

Para convertir fracciones mixtas negativas a fracciones impropias, se procede de la misma manera, y se obtendrá una fracción impropia negativa.

$-3\frac{7}{11}=\ \frac{\left(3\ast11\right)+7}{9}=-\ \frac{40}{11}$

Por tanto, la fracción mixta $-3\frac{7}{11}$ es igual a la fracción impropia $-\ \frac{40}{11}$ .

Bibliografía:
Matemáticas para 1.er curso de ESO. (2016). Santillana. Ministerio de Educación del Ecuador. (2016). Matemática 6° grado. Libro del estudiante. EDINUN Ediciones Nacionales Unidas. Zill, D. G., & Dewar, J. M. (2008). Precálculo con avances de cálculo. McGraw-Hill Interamericana.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Fracciones mixtas. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/fracciones-mixtas/). Última edición: febrero 2022. Consultado el 20 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!