Contenidos
Funciones trigonométricas
Relación entre los ángulos interiores y los lados de un triángulo.
Definición
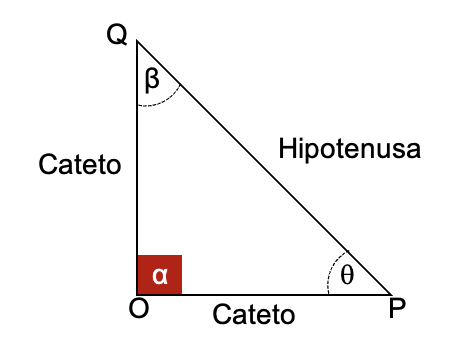
Las funciones trigonométricas refieren la relación entre los ángulos interiores y los lados de un triángulo.
En la definición básica de las funciones trigonométricas, relacionan los lados de un triángulo rectángulos solo para ángulos agudos, empleando el teorema de Pitágoras.
El ángulo del triángulo de referencia es el argumento o variable independiente a partir del cual se define el cociente de los lados asociados.
Las definiciones modernas expresan las funciones trigonométricas en la circunferencia como una extensión de las razones trigonométricas del triángulo rectángulo.
Permitiendo extender el dominio de las funciones seno y coseno a todo el plano complejo.
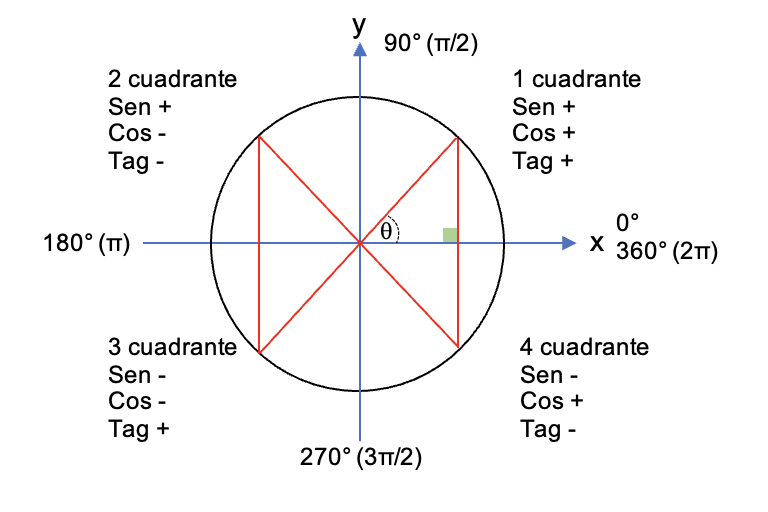
Esto se conoce como la circunferencia trigonométrica o círculo unitario, para hallar las relaciones trigonométricas para cualquier tipo de ángulo, no limitarlo sólo a ángulos agudos.
Características
- El seno, coseno y tangente son denominadas funciones primarias.
- La secante, la cosecante y la cotangente se derivan de las funciones de seno, coseno y tangente.
- La secante, la cosecante y la cotangente son denominadas funciones recíprocas de las funciones primarias.
- En el círculo unitario las funciones trigonométricas tienen diferentes signos numéricos (+ o -) en los diferentes cuadrantes, que se basan en el eje positivo o negativo del cuadrante.
- Las inversas de las funciones primarias adoptan el signo (+ o -) de su función primaria en cada cuadrante.
- Las funciones trigonométricas de Sinθ, Cosecθ son positivas en los cuadrantes I y II, y negativas en los cuadrantes III y IV.
- Todas las funciones trigonométricas tienen un rango positivo en el primer cuadrante.
- Las funciones trigonométricas Tanθ, Cotθ son positivas sólo en los Cuadrantes I y III,
- Las razones trigonométricas de Cosθ, Secθ son positivas sólo en los Cuadrantes I y IV.
Tipos
Para definir los tipos de funciones o razones trigonométricas se hará tomando como referencia el triángulo rectángulo.
El ángulo referente será θ, el cateto opuesto (a), cateto adyacente (b) y la hipotenusa es denotada como (c).
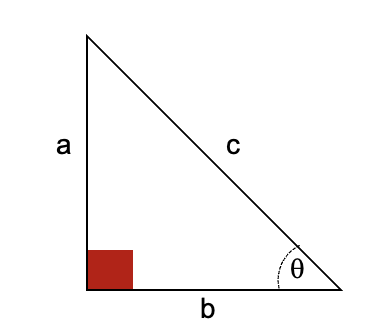
Seno: relaciona el cateto opuesto sobre la hipotenusa y se denota como (sen) o (sin). Su simbología es la siguiente:
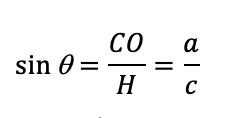
Coseno: esta función relaciona el cateto adyacente sobre la hipotenusa del triángulo. Se abrevia como (cos) y su fórmula es la siguiente:
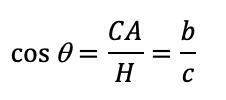
Tangente: La función relaciona el cateto opuesto sobre el cateto adyacente. A diferencia de las dos funciones anteriores no relaciona la hipotenusa.
Se indica como (tan) y su fórmula es:
![]()
Una particularidad de la tangente es que, si se conocen los valores de coseno y seno, entonces la tangente también se puede determinar dividiendo el seno por el coseno.
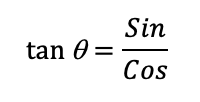
Cosecante (csc): es el recíproco del seno, lo que significa que en lugar de que su razón sea el lado opuesto sobre la hipotenusa, sería la hipotenusa sobre el cateto opuesto.
![]()
Secante (sec): es la función inversa del coseno, por lo que la secante del ángulo q sería la hipotenusa dividida por el cateto adyacente.
![]()
Cotangente (Cot): es el recíproco de la tangente, es decir; que la cotangente del ángulo q es igual al cateto adyacente dividido por el cateto opuesto.
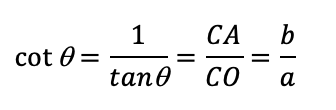
Considerando el círculo trigonométrico se pueden definir los valores de las seis funciones trigonométricas para θ en términos de las coordenadas x e y.
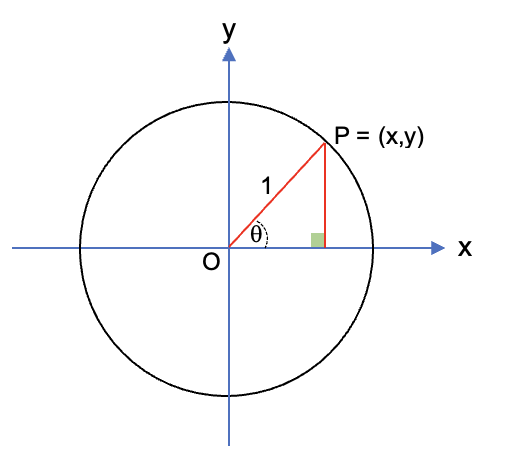 |
sinθ = y cosθ = x tanθ = cscθ = secθ = cotθ = |
Valores
Las funciones trigonométricas tienen un dominio q, que está en grados o radianes y del círculo unitario se pueden derivar los principales valores de las diferentes funciones trigonométricas dependiendo de q.
Como se mencionó anteriormente, las funciones trigonométricas no se limitan a un ángulo agudo.
A continuación, se muestra la tabla trigonométrica.
| θ | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| Sin θ | 0 | 1 | 0 | -1 | 0 | |||
| Cos θ | 1 | 0 | -1 | 0 | 1 | |||
| Tan θ | 0 | 1 | No definida | 0 | No definida | 0 | ||
| Csc θ | No definida | 2 | 1 | No definida | -1 | No definida | ||
| Sec θ | 1 | 2 | No definida | -1 | No definida | 1 | ||
| Cot θ | No definida | 1 | 0 | No definida | 0 | No definida |
Ejercicios resueltos
Ejercicio #1
Utilizando la tabla trigonométrica hallar los valores de csc 45°, sin 60° y tan 30°
Ver solución
- csc 45° =
- sin 60° =
- tan 30° =
Ejercicio #2
Hallar las medidas de los ángulos y lados faltantes del triángulo de la figura.
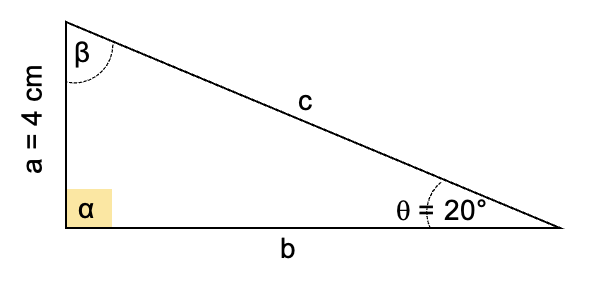
Ver solución
Por propiedad de los ángulos internos del triángulo se conoce que α + β + q = 180°, despejando:
β = 180° – (θ + α) = 180° – (20° + 90°) = 180° – 110°
β = 70°
Se puede hallar la hipotenusa (c) usando la razón trigonométrica seno
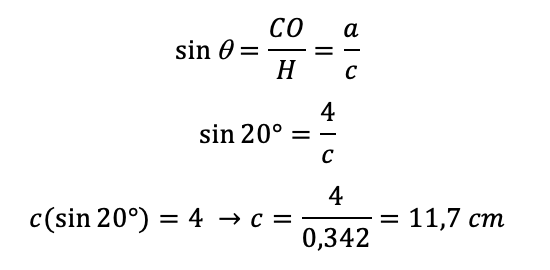
La hipotenusa es igual a 11,70 cm.
Para encontrar el valor del cateto adyacente se puede usar el coseno
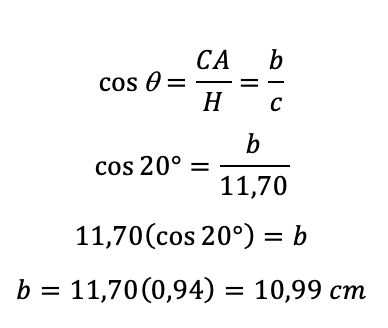
El cateto adyacente es igual a 10,99 cm.
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana