Contenidos

Inicio / Historia y Sociedad / Triángulo rectángulo

Matemática

Geometría

Triángulo rectángulo

Triángulo que tiene un ángulo igual a 90° o ángulo recto.

Por

Haude Medina

Tabla de contenidos:

Definición

Se define como triángulo rectángulo aquel triángulo que tiene un ángulo igual a 90° o ángulo recto.

El triángulo rectángulo pertenece a los polígonos irregulares de tres lados y es clasificado en los triángulos por la medida de sus ángulos.

En la figura se muestra un triángulo rectángulo con los siguientes elementos:

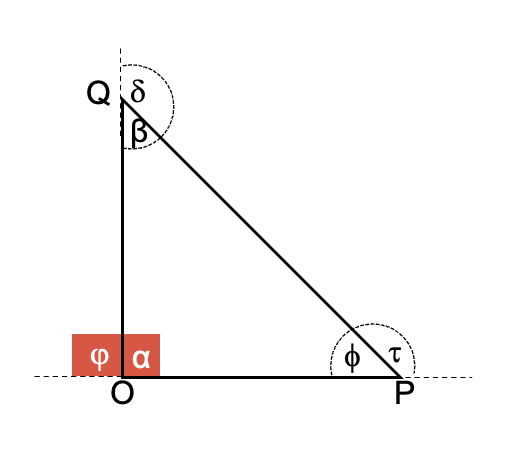
Figura de un triángulo rectángulo.

Vértices: son los puntos O, P, Q.
Lados: son los segmentos de recta que forman el triángulo, denotados como: $\overline{OP}$ , $\overline{PQ}\$ y $\overline{QO}$ . En este tipo de triángulo, los lados reciben nombres específicos por el Teorema de Pitágoras. Así, el lado $\overline{PQ}$ es la hipotenusa y los lados $\overline{OP}$ y $\overline{QO}$ son los catetos.
Ángulos internos: formado por α,Φ,β, donde se cumple que α + Φ + β = 180°.
Ángulos externos: están denotados por δ, φ, τ, cada uno es suplementario al ángulo interno de mismo lado. Se cumple que el ángulo externo adyacente al ángulo recto interno, también mide 90°.

El estudio de los triángulos rectángulos es de gran importancia en la geometría, por sus propiedades especiales, que permiten resolver diversas situaciones de polígonos, que se pueden estudiar trazando en ellos triángulos rectángulos.

Características

Como se ha mencionado, este tipo de triángulo tiene características especiales entre las que se pueden mencionar.

Tiene un ángulo recto, y los otros dos ángulos son complementarios debido a que su suma es igual a 90°. Como α = 90°, entonces Φ + β = 90°, son complementarios.
Sus ángulos internos son un ángulo recto y dos ángulos agudos. Nunca tiene un ángulo obtuso.
Este tipo de triángulos da origen al «Teorema de Pitágoras», donde ${\overline{(PQ})}^2={\overline{(OP})}^2+\ {\overline{(QO})}^2$ , dando nombre a cada uno de los lados del triángulo rectángulo.
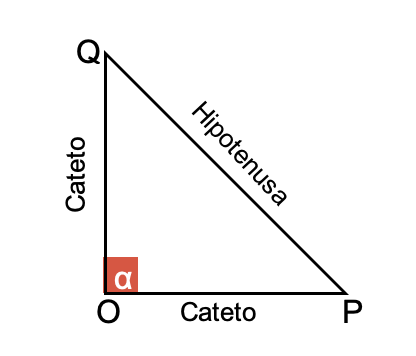
El lado opuesto al ángulo recto se conoce como hipotenusa (según el teorema de Pitágoras) y es el de mayor longitud.
Los lados adyacentes al ángulo recto reciben el nombre de catetos. Si la altura que se traza desde el ángulo recto concurre con uno de los catetos, se considera que un cateto es la base y el otro es la altura del triángulo. De esta manera se pueden trazar dos alturas que cada una coincide con un cateto: $h_{(QO)}$ y $h_{(OP)}$ .
La altura que se traza desde el ángulo recto hasta la hipotenusa, divide el triángulo en dos semejantes entre sí y semejante al original. Por tanto $\triangle OPQ\sim\triangle OPH\sim\triangle OHQ$ .
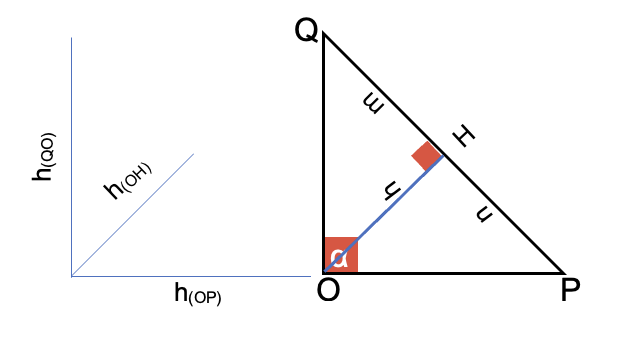
De la característica anterior se origina al «teorema de la altura», donde:
$\frac{n}{h}=\frac{h}{m}\Rightarrow h^2=n\ast m\Rightarrow h=\sqrt{n\ast m}$ .
A partir de un triángulo rectángulo se definen las funciones trigonométricas, seno, coseno, tangente y cada una de sus inversas.
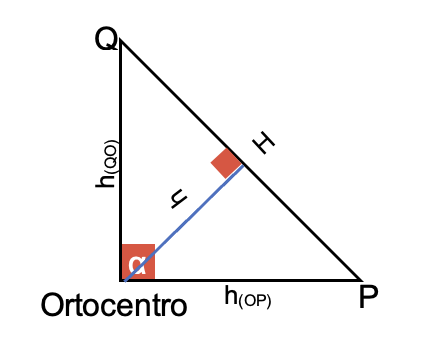
El ortocentro, donde concurren las tres alturas, es el vértice del ángulo recto.

Tipos

Los triángulos rectángulos se pueden definir dos tipos de triángulos, considerando la peculiaridad del ángulo recto y la medida de sus lados.

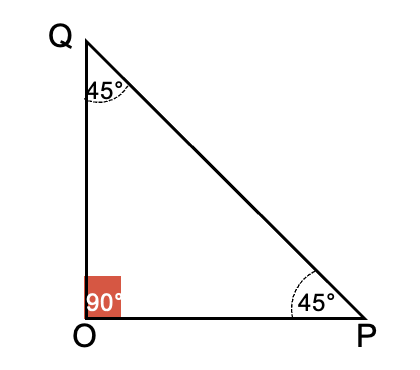
Publicidad, continua debajo

Triángulo rectángulo isósceles: este tipo de triángulo tiene la particularidad de tener los dos catetos de igual longitud, $\overline{OP}=\overline{QO}$ . Sus ángulos son uno ángulo recto y dos ángulos agudos cada uno de 45°.
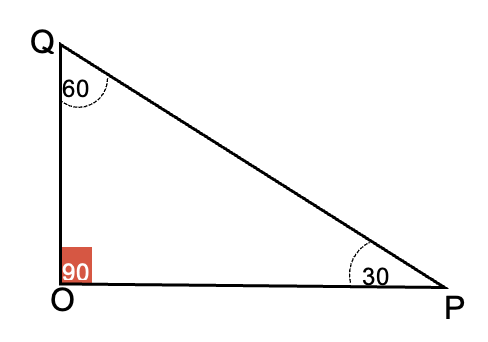
Triángulo rectángulo escaleno: entre sus características se encuentran que sus tres lados y sus tres ángulos son de distintas medidas. La hipotenusa mide el doble del cateto menor y el cateto mayor $\sqrt3$ veces la longitud del cateto. Este tipo de triángulo tiene un caso especial cuando sus ángulos interiores tienen miden 30°, 60° y 90°, cada uno.

Perímetro y área

Perímetro

El perímetro de un triángulo rectángulo se halla sumando la medida de cada uno de sus lados

$P=l_1+l_2+l_3$

Para el triángulo que se ha estado analizando los lados están representados por los segmentos de recta $\overline{OP}$ , $\overline{PQ}$ , $\overline{QO}$ , por lo que para este caso el perímetro sería:

$P=\overline{OP}+\overline{PQ}+\overline{QO}$

Cuando se desconoce la medida de alguno de sus lados, por lo general, se utiliza el teorema de Pitágoras, teorema de la altura o las funciones trigonométricas para hallar su longitud.

Área

El área puede ser calculada con la siguiente fórmula:

$A=\frac{b\ast h}{2}$

Donde:

A: es el área del triángulo
h: es la medida de la altura
b: es la medida de la base

Ejercicios resueltos

Ejercicio #1

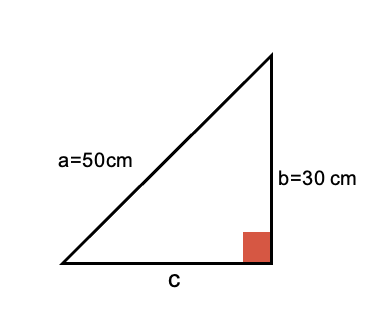
Problema a resolver: en el siguiente triángulo se conoce que el lado opuesto al ángulo recto mide 50 cm. y otro de sus lados mide 30 cm. ¿Cuál es la medida del perímetro?

Ejercicio de triángulo rectángulo.

Ver solución

Para hallar el perímetro se debe conocer la medida del lado c, que es otro de los catetos, el cual se puede conocer aplicando el teorema de Pitágoras donde.

$a^2 = b^2 + c^2$ , despejando se obtiene que:

$c^2=a^2-b^2\Rightarrow c=\sqrt{a^2-b^2}$

$c=\sqrt{{50}^2-{30}^2}=\sqrt{2500-900}=\sqrt{1600}$

$c=40\ cm$

Conocido la medida de los tres lados el perímetro se halla de la forma siguiente:

$P=a+b+c$

$P=50+30+40=120\ cm$

Ejercicio #2

Problema a resolver: hallar el área de un triángulo rectángulo cuya base mide 5 metros y la altura 12 metros.

Ver solución

Aplicando la fórmula conocida del área se tiene:

$A=\frac{b\ast h}{2}\ \Rightarrow A=\frac{5\ast12}{2}$

$A=\frac{5\ast12}{2}=\frac{60}{2}$

$A=30{\ metros}^2$

El área del triángulo es de 30 metros².

Ejercicio #3

Problema a resolver: se tiene un triángulo rectángulo del cual se conoce que el área es de 24 cm² y la base es de 8 cm. ¿Cuál es la medida de la altura, si se sabe que esta coincide con uno de los lados?

Ver solución

Partiendo de que la altura coincide con uno de los lados del triángulo rectángulo, se puede aplicar la fórmula del área para calcular la altura.

$A=\frac{b\ast h}{2}$

despejando la altura se tiene

$h=\frac{2A}{b}=\frac{2\left(24\right)}{8}$

$h=\frac{48}{8}=6\ cm$

La altura del triángulo rectángulo es igual a 6 centímetros.

Bibliografía:
Briones, L. (2010). Geometría secuencial para la educación básica. Universidad de Chile. Ministerio de Educación del Ecuador. (2016). Matemática 9° grado. Libro del estudiante. SMEcuaediciones. Zahner, B. (2013). Trigonometría del triángulo rectángulo. Editorial CK-12.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Triángulo rectángulo. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/triangulo-rectangulo/). Última edición: abril 2022. Consultado el 18 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!