Contenidos
Ángulos internos
Ángulo que se forma dentro de un polígono cuando se intersecan dos de sus lados adyacentes.
Definición
Un ángulo interno o interior en geometría, es el ángulo que se forma dentro de un polígono cuando se intersecan dos de sus lados adyacentes.
Los ángulos internos también se forman cuando dos rectas paralelas son cortadas por una transversal.
De esta manera se puede distinguir dos tipos de ángulos internos:
- Ángulos internos dentro de un polígono, ya sea regular o irregular.
- Ángulos internos que se forman dentro del área cerrada de dos rectas paralelas al ser cortadas por una transversal.
En las figuras a continuación se muestran son dos ejemplos de ángulos interiores.
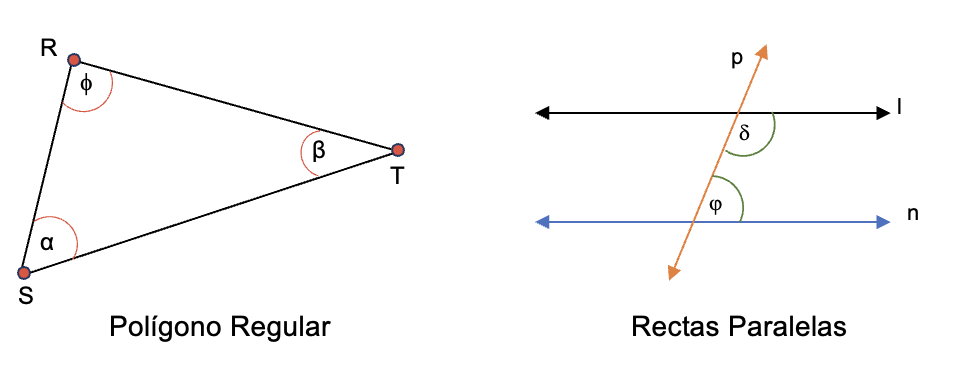
En el triángulo se identifican los tres ángulos internos α, β, Φ, y en las rectas paralelas se pueden observar los ángulos φ, δ.
Propiedades
Las propiedades de los ángulos internos dependen de si pertenecen a un polígono o si se forman cuando una transversal corta a dos rectas paralelas. A continuación, se mencionan sus propiedades.
Publicidad, continua debajoPropiedades ángulos internos de un polígono
- El número de ángulos internos es igual al número de lados del polígono.
- Los ángulos internos de un polígono regular tienen la misma medida.
- La suma de los ángulos internos de cualquier polígono de “n” lados, se halla mediante la fórmula: Suma de ∠ = (n – 2) * 180°.
- Si se conoce la suma de todos los ángulos interiores de un polígono regular, se puede obtener el ángulo interior con la fórmula:
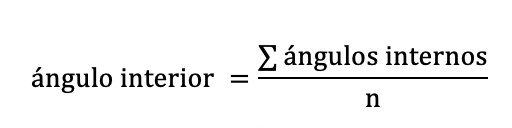
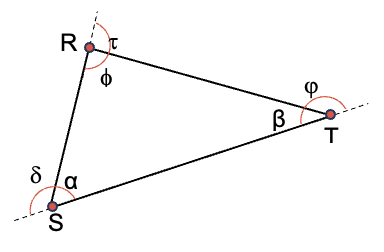
- En cualquier polígono el ángulo interno es suplementario al ángulo externo del mismo lado. En la figura se tiene que: Φ + τ =180°, α + δ = 180°, β + φ = 180°.
Utilizando las fórmulas dadas, en la siguiente tabla se muestra la relación de la suma de los ángulos internos y la medida de cada ángulo interior de varios polígonos regulares conocidos.
| Polígono | No. de lados | Suma ángulos internos | Medida cada ángulo interno |
| Triángulo | 3 | Σ∠ = (3 – 2) * 180° = 180° | Ángulo interno = 180°/3 = 60° |
| Cuadrilátero | 4 | Σ∠ = (4 – 2) * 180° = 360° | Ángulo interno = 360°/4 = 90° |
| Pentágono | 5 | Σ∠ = (5 – 2) * 180° = 540° | Ángulo interno = 540°/5 = 108° |
| Hexágono | 6 | Σ∠ = (6 – 2) * 180° = 720° | Ángulo interno = 720°/6 = 120° |
| Heptágono | 7 | Σ∠ = (7 – 2) * 180° = 900° | Ángulo interno = 900°/7 = 128,57° |
| Octágono | 8 | Σ∠ = (8 – 2) * 180° = 1080° | Ángulo interno = 1080°/8 = 135° |
Propiedades ángulos internos entre paralelas
Se forman varios tipos de ángulos internos:
- Los ángulos alternos internos:
- Los ángulos alternos internos son los ángulos formados en los lados opuestos de la transversal.
- Los ángulos alternos internos tienen la misma medida.
- La condición anterior, permite comprobar que dos líneas dada sean paralelas.
- Los ángulos interiores consecutivos:
- Los ángulos interiores consecutivos se encuentran en el mismo lado de la transversal y no son adyacentes.
- Los ángulos interiores consecutivos tienen vértices diferentes y comparten un lado en común.
- La suma de los ángulos internos consecutivos es de 180°.
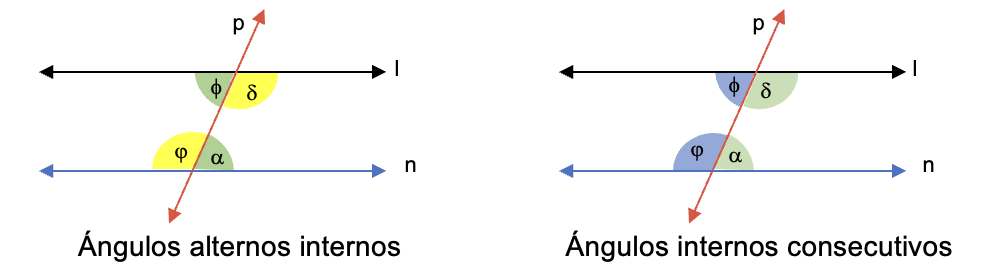
En la primera figura los ángulos Φ y α son alternos internos y el ángulo δ es alterno interno con φ.
La segunda figura los ángulos internos consecutivos son Φ y φ. Y el otro par de internos consecutivos son los ángulos δ y α.
Ejercicios resueltos
Ejercicio #1
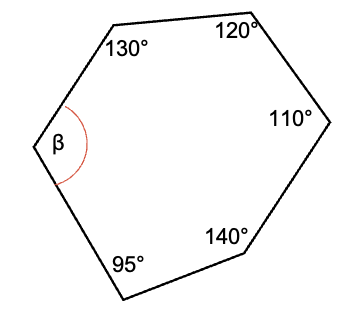
Problema a resolver: hallar la medida del ángulo β del hexágono.
Ver solución
Por ser el polígono un hexágono se conoce que la suma de sus ángulos internos es:
Σ∠ = (6 – 2) * 180° = 720°
Por lo que
β + 130° + 120° + 110° +140° + 95 = 720°.
Realizando la suma de los ángulos: β + 595° = 720°.
Despejando β → β = 720° – 595°.
β = 125°. El valor del ángulo β es de 125°.
Ejercicio #2
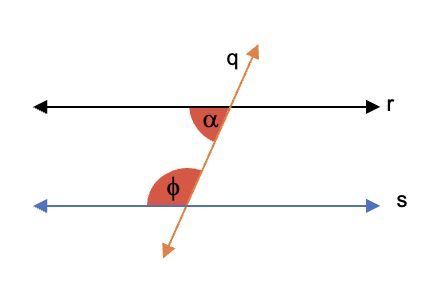
Problema a resolver: se conoce la medida del ∠α = 35°, hallar la medida del ángulo Φ, si se sabe que ambos son internos consecutivos entre las paralelas dadas.
Ver solución
Por propiedad, la suma de los ángulos internos consecutivos de las paralelas r, s, es igual a 180°. Por tanto, conocida la medida del ∠α, se puede desarrollar la ecuación:
∠α + ∠Φ = 180°
Despejando ∠Φ → ∠Φ = 180° – ∠α
Se sustituye el valor del ángulo conocido para obtener:
∠Φ = 180° – 35° = 145°
La medida de los ángulos internos consecutivos es: ∠α = 35° y ∠Φ = 145°.
Ejercicio #3
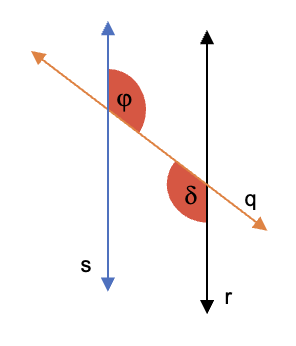
Problema a resolver: En la siguiente figura se sabe que el ∠φ y ∠δ son ángulos alternos internos. Hallar la amplitud de ∠φ, si ∠δ = 115°.
Ver solución
Por propiedad de los ángulos alternos internos entre paralelas cortadas por una transversal, se conoce que la medida de ambos es la misma, por lo tanto:
∠φ =∠δ = 115°
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana