Contenidos

Inicio / Matemática / Geometría / Teorema de Pitágoras

Matemática

Geometría

Teorema de Pitágoras

Enunciado matemático que relaciona los lados de un triángulo rectángulo.

Por

Haude Medina

Tabla de contenidos:

Definición

El teorema de Pitágoras, es un enunciado matemático que relaciona los lados de un triángulo rectángulo, permitiendo calcular alguna de sus longitudes, conociendo la medida de dos de ellas. Se aplica únicamente a los triángulos rectángulos.

El teorema de Pitágoras, debe su nombre, al matemático y filósofo griego Pitágoras, quien es considerado como el primer matemático puro y dejó diversos aportes a la aritmética, la geometría y otras áreas de la ciencia.

Se llama teorema, por ser una proposición de una fórmula, que se puede demostrar como verdadera, a través de operaciones matemáticas y diferentes argumentos lógicos.

El matemático Pitágoras, en su teorema, se refiere a la relación de los lados de un triángulo rectángulo, pero hace su planteamiento basándose en los cuadrados que se forman a partir de cada uno de los lados de este triángulo.

Asignándole, un nombre a cada lado del triángulo rectángulo, siendo la hipotenusa el lado opuesto al ángulo recto y el lado de mayor longitud, y los otros dos lados reciben el nombre de catetos.

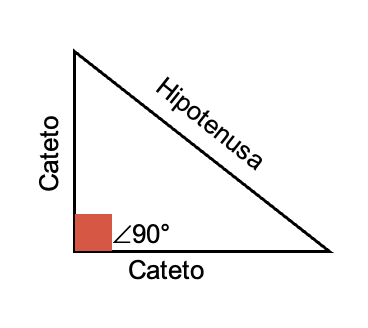
Triángulo del Teorema de Pitágoras.

Entonces, según el teorema de Pitágoras, el área del cuadrado construido sobre la hipotenusa, es igual a la suma de las áreas de los cuadrados construidos sobre los catetos.

Publicidad, continua debajo

Para comprender lo formulado por Pitágoras, se le asignará a cada lado del triángulo rectángulo una letra cualquiera, para este caso serán “a”, “b”, “c”. Así, la medida de la hipotenusa es “c”, el cateto1 su medida será “a” y el cateto2 con medida “b”.

Según el teorema de Pitágoras, en la representación gráfica, se debe cumplir que $c^2=a^2+b^2$ .

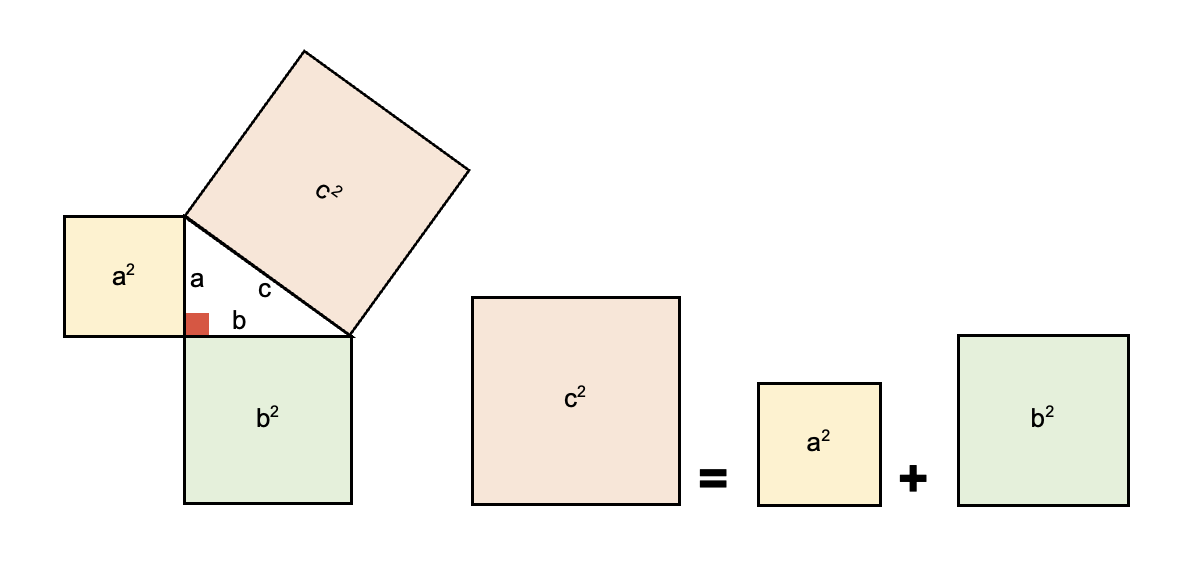
Cuadrados del Teorema de Pitágoras.

Esta fórmula, además, permite verificar que un triángulo sea verdaderamente rectángulo, ya que se debe comprobar la relación matemática. Esto es lo que se conoce como “Recíproco del Teorema de Pitágoras”.

Por ejemplo, supóngase que se tiene un triángulo rectángulo cuya hipotenusa es 13 cm. y cada uno de los catetos miden 5 cm. y 12 cm. Para comprobar que sea un triángulo rectángulo se evalúan los valores en la ecuación pitagórica y se debe dar que: $c^2=a^2+b^2$ .

${13}^2=5^2+{12}^2$

$169=25+144$

$169=169$

De esta manera, se comprueba que las medidas de los lados dadas corresponden a un triángulo rectángulo.

Fórmula y resolución

De la explicación anterior, se conoce el enunciado del Teorema de Pitágoras, con el cual es posible calcular la medida de la hipotenusa, conocida la longitud de sus catetos, o de forma general cualquiera de los lados del triángulo rectángulo. La fórmula es:

$c^2=a^2+b^2$

Donde:

“a”, “b”: representan cada uno de los catetos.
“c”: corresponde a la hipotenusa del triángulo rectángulo.

El teorema de Pitágoras se puede aplicar de manera directa, es decir, conocida las medidas de los catetos, calcular el valor de la hipotenusa, para lo que se usa la fórmula ya enunciada para obtener que:

$c^2=a^2+b^2\longrightarrow c=\sqrt{a^2+b^2}$

Por ejemplo, si se tiene un triángulo rectángulo con las medidas que se indican en la figura, se puede hallar el valor de la hipotenusa.

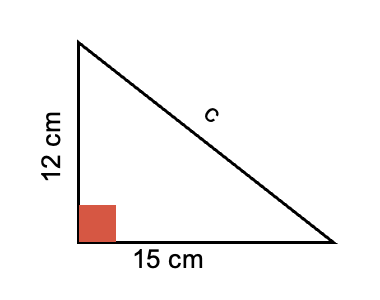
Fórmula y resolución del Teorema de Pitágoras.

Partiendo de la fórmula $c=\sqrt{a^2+b^2}$ , se sustituyen las medidas de los catetos indicadas y se obtiene que el valor de la hipotenusa es 19,2093 cm.

$c=\sqrt{{12}^2+{15}^2}$

$c=\sqrt{144+225}\longrightarrow c=\sqrt{369}$

$c=19,2093\ cm$

Otro caso es, hallar la medida de uno de los catetos si se sabe la medida de la hipotenusa y del otro cateto.

Para realizar estos cálculos, se puede despejar de la fórmula “a” o “b”, según sea el caso.

$c^2=a^2+b^2\longrightarrow a^2=c^2-b^2$
$a=\sqrt{c^2-b^2}$
$c^2=a^2+b^2\longrightarrow b^2=c^2-a^2$
$b=\sqrt{c^2-a^2}$

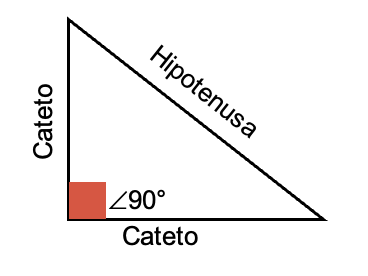En figuras geométricas planas, se puede aplicar el teorema de Pitágoras, siempre y cuando se forme un triángulo rectángulo, que permita la aplicación del teorema.

Esto da la posibilidad de hallar, por ejemplo; la altura de un triángulo, de un trapecio, entre otras figuras, aplicar la semejanza de triángulos, hallar la medida de un lado de la figura desde el valor de la altura.

Ejercicios resueltos

Ejercicio #1

Problemas a resolver: los lados de un triángulo miden 15 cm, 8 cm y 12 cm. ¿Las medidas corresponden a un triángulo rectángulo?

Ver solución

Para saber si las medidas dadas corresponden a un triángulo rectángulo, se aplica el Recíproco del Teorema de Pitágoras, que no es más que verificar que se cumpla que:

$c^2=a^2+b^2$

Sustituyendo las medidas del triángulo se tiene que:

${15}^2=8^2+{12}^2$

$225=64+144$

$225\neq208$

No se verifica la igualdad, por tanto, las medidas dadas no corresponden a un triángulo rectángulo.

Ejercicio #2

Problema a resolver: el triángulo de la figura muestra la medida de la hipotenusa y de uno de los catetos. Encuentre la medida del otro cateto usando la fórmula del teorema de Pitágoras.

Imagen de ejercicio de Teorema de Pitágoras.

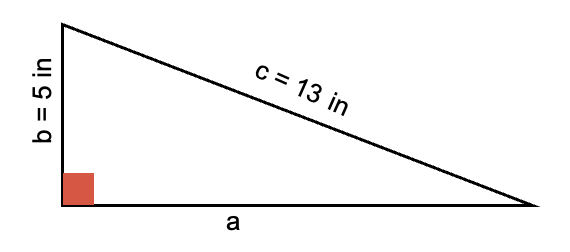
Ver solución

Para hallar el cateto “a” se utiliza la fórmula:

$a=\sqrt{{13}^2-5^2}$

$a=\sqrt{169-25}$

$a=\sqrt{144}$

$a=12\ in$

El valor del cateto “a” es de 12 in.

Ejercicio #3

Problema a resolver: del siguiente triángulo se debe encontrar la medida del lado faltante.

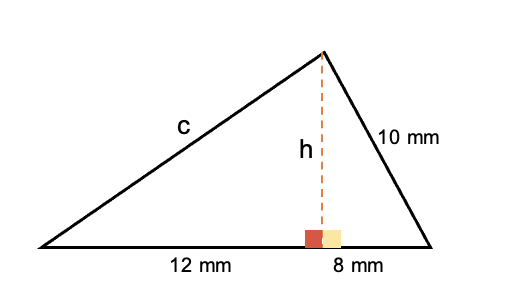
Imagen de ejercicio de Teorema de Pitágoras

Ver solución

La altura (h) divide el triángulo en dos triángulo rectángulos con un lado común que es “h”, permitiendo aplicar el teorema de Pitágoras.

Ahora bien, se puede hallar el valor de la altura utilizando los valores de los lados del triángulo rectángulo que se forma a la derecha para posteriormente, hallar el lado “c” del triángulo rectángulo que se forma a la izquierda.

Paso 1) Hallar “h”

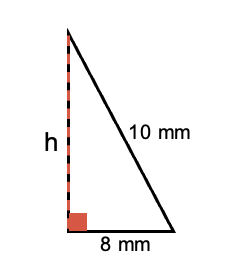
Hallar h para el Teorema de Pitágoras.

La hipotenusa es 10 mm, el cateto mide 8 mm.

$h=\sqrt{{10}^2-8^2}$

$h=\sqrt{100-64}=\sqrt{36}$

$h=6\ mm$

Paso 2) hallar «c»

Para el triángulo de la izquierda ahora se conoce el valor de los dos catetos y se puede calcular la medida de la hipotenusa “c”.

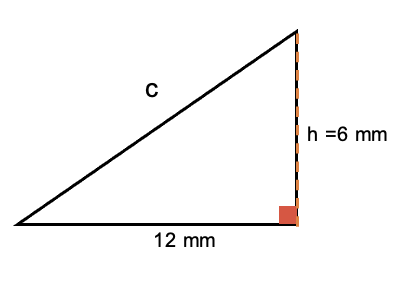
Hallar la hipotenusa en Teorema de Pitágoras.

La hipotenusa (c), los catetos miden 12 mm y 6 mm, respectivamente.

$c=\sqrt{{12}^2+6^2}$

$c=\sqrt{144-36}=\sqrt{180}$

$c=13,42\ mm$

Dando respuesta al problema planteado, la longitud del lado “c” del triángulo es de 13,42 mm.

De esta manera se puede aplicar el teorema de Pitágoras a un triángulo no rectángulo.

Bibliografía:
Iriondo, M. (s/f). Aprendiendo Matemáticas. Instituto Universitario Aeronáutico. Córdoba – Argentina. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador. Ministerio de Educación del Ecuador. (2016). Matemática 9° grado. Libro del estudiante. SMEcuaediciones.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Teorema de Pitágoras. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/teorema-de-pitagoras/). Última edición: mayo 2024. Consultado el 18 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!