Números reales

Definición

Los números Reales, se denotan con la letra (R) y se definen como el conjunto de números que agrupa o incluye los números naturales (N), enteros (Z), racionales (Q) e irracionales (I).

También se puede decir, que cualquier número racional o irracional es un número real, R = Q ∪ I.

Por esta razón, se dice que todos los números pertenecen al conjunto R, excluyendo los números complejos. Tampoco son números reales:

• Las fracciones del tipo , ya que la división por cero no está definida. Por ejemplo .
• La raíz cuadrada de un número negativo , por no estar definida dentro de los números reales. .
• La raíz par de cualquier número negativo de la formar , donde «n»es un número par. .

El conjunto de los números reales tiene varias características, se dice con infinitos R ∈ (-∞,+∞). Siguen un orden y se pueden representar en la recta real. Por último, pueden ser expresados como un número decimal.

Por ejemplo, 4 se puede expresar como decimal 4,00. La fracción se expresa como el decimal 0,6. La raíz de un número; es igual a 8,062.

Propiedades

El conjunto de los números reales (R), también satisface a diferentes propiedades de la matemática y se encuentran:

• Propiedad de cierre o cerradura: dice que la suma o multiplicación de dos números reales, siempre da como resultado un número real. Entonces para la suma, si a + b = c, c ∈ R. Ejemplo: 12 + 7 = 19, donde 19 pertenece a los números reales. Para la multiplicación, si a * b = c, c ∈ R. Ejemplo: 3 * 8 = 24, entonces 24 es también un número real.
• Propiedad conmutativa: el resultado de una suma o multiplicación es siempre igual, sin importar el orden en que se encuentren los números. Para la suma a + b = b + a, por tanto en la multiplicación a * b = b * a.
• Propiedad asociativa: la manera como se agrupen los números en una suma o multiplicación, no altera el resultado obtenido. Por tanto, en la suma (a + b) + c = a + (b + c) y para la multiplicación: (a * b) * c = a * (b * c).
• Propiedad distributiva: refiere que la multiplicación de un número por una suma o resta, es igual a la suma o diferencia de sus productos. Donde a(b ± c) = (a * b) ± (a * c).
• Propiedad modulativa o elemento neutro: en el caso de la suma, a cualquier número que se le sume 0, el resultado es igual al mismo número (a + 0 = a). En cambio, para la multiplicación cualquier número que se multiplique por 1, da como resultado el mismo número (a * 1 = a).

Clasificación y tipos

Como se ha estudiado, el conjunto R, está formado por varios subconjuntos. En la imagen, se observa los 5 subconjuntos de números que pertenecen a los números reales.

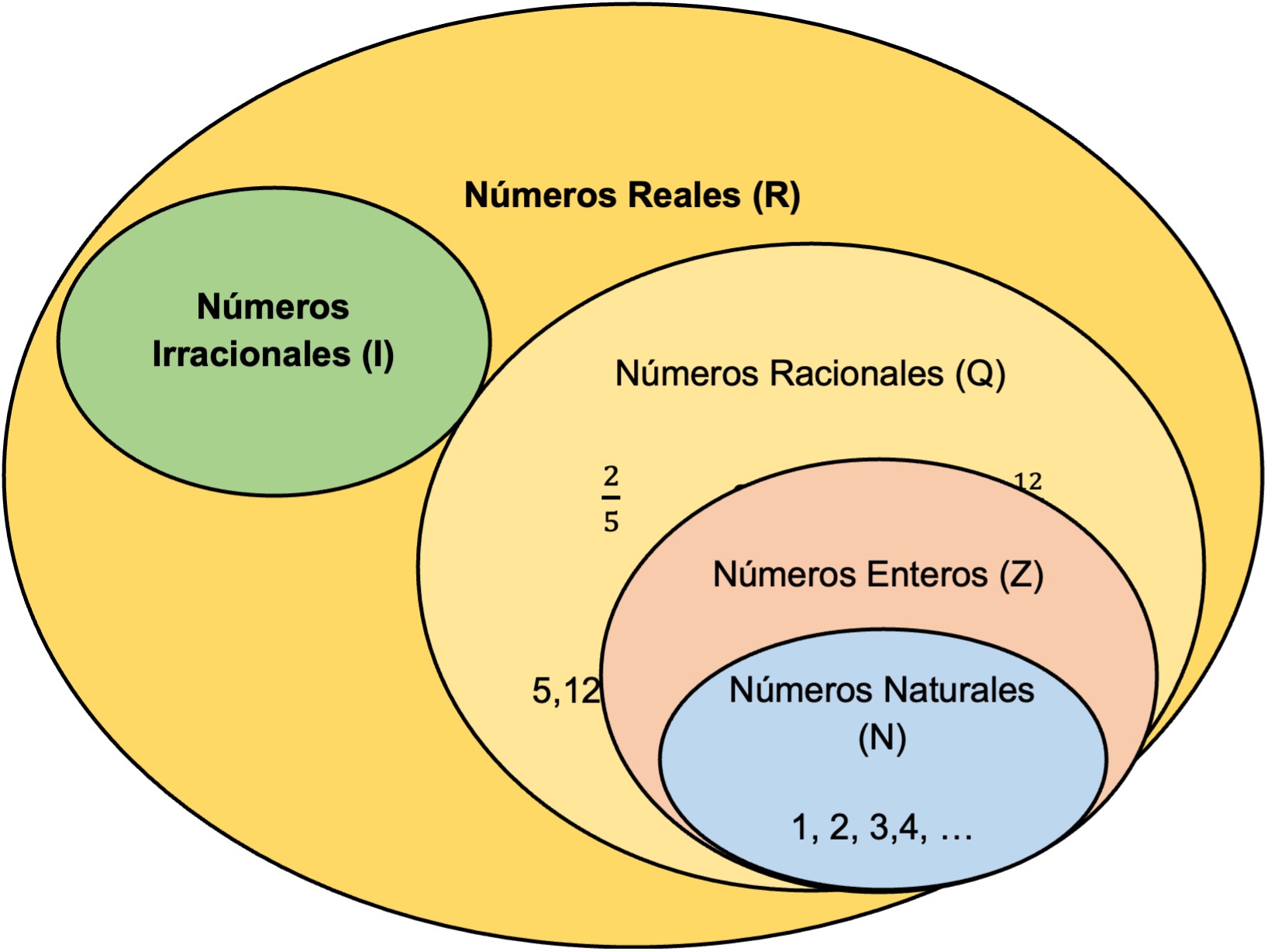
Conjunto de números reales.

• Números naturales: se indican con la letra N. Son los números no decimales mayores de 0. Pertenecen a este conjunto N = (1, 2, 3, 4, 5, 6, 7,…).
• Números enteros: el conjunto de los números enteros se identifica con la letra Z. Está formado por los números naturales y sus opuestos, es decir; por sus números negativos e incluye al 0. Donde Z = (-9, -8, -7, …, 0, 1, 2, 3, …). Estos números no tienen parte decimal ni fraccionaria.
  Los números naturales están comprendidos dentro de los números en enteros.
• Números racionales: son todos aquellos números que pueden ser escritos como una fracción de números enteros, donde el denominador debe ser diferente de 0. El conjunto de los racionales se denota con la letra Q = , , . El resultado de la fracción puede ser un número entero, decimal finito o semiperiódico.
• Números irracionales: su propio nombre lo indica, que no son racionales, por tanto, se definen como aquellos números que no pueden ser expresados como una fracción de números enteros. Son decimales que no se expresan ni de manera exacta ni periódica. Se identifican con la letra I = (, π, Φ, …)

Ejemplos

Algunos ejemplos de números reales según su clasificación son:

Números naturales	1, 2, 3, 4, 5, 6, 7, 8, ….
Números enteros	-9, -8, -7, …, 0, 1, 2, 3, …
Números racionales	, , ,
Números irracionales	, β

Ejercicios resueltos

Ejercicio #1

A continuación se listan una serie de números, indicar cuál es el menor conjunto de números reales que pertenece:

Número	Conjunto
167
Φ
-157
4,134134
π

Ver solución

Número	Conjunto
167	Números naturales.
	Números racionales.
Φ	Números irracionales. Es conocido como número Áureo.
-157	Números enteros, por ser negativo.
	Números irracionales.
	Números naturales. La raíz cúbica de 27 es igual a 3, por tanto el menor conjunto al que pertenece al conjunto N.
4,134134	Números racionales. La parte decimal es periódica.
π	Números irracionales. Es la constante Pi.

Ejercicio #2

Se listan una serie de operaciones. Indicar que propiedad de los números reales se aplica.

Operación matemática	Propiedad
25 + 0 = 25
121 * 9 = 9 * 121
4,67 * 1 = 4,67

Ver solución

Operación matemática	Propiedad
	Propiedad asociativa.
25 + 0 = 25	Propiedad modulativa de la suma.
121 * 9 = 9 * 121	Propiedad conmutativa.
	Propiedad distributiva.
4,67 * 1 = 4,67	Propiedad modulativa de la multiplicación.