Contenidos
Polinomios
Expresión algebraica formado por la combinación de términos que están unidos mediante operaciones de suma o resta.
Definición
El álgebra es la rama de las matemáticas que estudia los polinomios y lo define como una expresión algebraica formado por la combinación de varios términos que están unidos entre sí mediante operaciones de suma o resta.
También se puede definir un polinomio como la suma de varios monomios no semejantes.
La palabra polinomio proviene de las palabras griegas “poli” que significa muchos y “nomio” que quiere decir término, así que polinomio es “muchos términos”.

Aunque un polinomio es una expresión algebraica, no todas las expresiones algebraicas son polinomios. Entonces, para que una expresión algebraica sea considerada como un polinomio debe cumplir con las siguientes características:
- Los exponentes de las variables deben ser números positivos no negativos.
- No debe haber variables en el denominador de fracciones que aparezcan en algún término.
- Las variables no deben estar dentro de radicales.
Por tanto, no son polinomios las expresiones algebraicas como ,
,
,
.
Un polinomio se puede denotar como una función polinomial de la forma siguiente: P(x) = 4x2 – 3x + 2. Se trata de funciones continuas cuyo dominio es el conjunto de los números reales
Publicidad, continua debajoPartes
En los polinomios se pueden identificar varios elementos que lo conforman y que se muestran y definen a continuación.
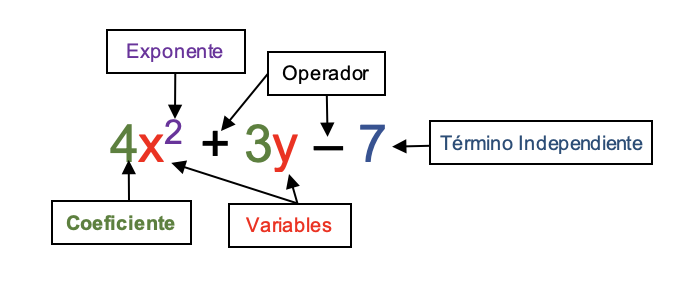
- Términos: es cada uno de los monomios que conforman el polinomio y que están separados por los operadores matemáticos. Por ejemplo, 4x2, 3y, 2.
- Variable: es también llamada incógnita y es una letra que se utiliza para representar un número desconocido y que puede tomar diferentes valores dentro del conjunto de los reales.
- Coeficiente: es cualquier valor dentro de los reales, diferente de 0, que precede a la variable. En el ejemplo los coeficientes son los números 4 y 3.
- Exponente: es el número al cual está elevada la variable. El exponente debe ser un número entero positivo Z(+) = {0, 1, 2, 3, …). El exponente tiene varias particularidades:
- determina el grado del polinomio.
- cuando el exponente es 0 la variable no se escribe. 5x0 = 5(1) = 5.
- cuando el exponente es 1, por lo general se omite. 5x1 = 5x.
- Permite ordenar un polinomio, lo que se conoce como escribir un polinomio en su forma estándar. Por lo que se conoce como forma estándar cuando los términos se arreglan desde el de mayor grado hasta el de menor grado.
- Grado de un polinomio: se define como el mayor grado de un monomio dentro de un polinomio y viene dado por el mayor exponente de la variable. Por ejemplo, 4x2 + 3y – 7, el grado es 2. Se distinguen dos tipos de grado.
- Grado absoluto (GA): Si el término del polinomio contiene varias variables el grado absoluto resulta de sumar los exponentes de las variables. El término de mayor grado absoluto es aquel cuya suma de exponentes sea mayor. Por ejemplo; 5x2y4 el grado absoluto es 2 + 4 = 6.
- Grado relativo (GR): en cada término corresponde al mayor exponente de cada variable, así se tiene que para 5x2y4 + 5x3y3, el grado relativo de x es 3, el de y es 4.
- Término Independiente: es aquel donde no está presente la variable, el -7 es el término independiente del ejemplo.
Tipos y clasificación
Hay nombres específicos que se usan para describir los polinomios con una cierta cantidad de términos.
Por el número de términos se nombran de la siguiente forma:
- Binomio: es una expresión polinomial que contiene sólo dos términos.
- Trinomio: es la expresión polinomial que contiene únicamente 3 términos.
- Polinomio: cuando la expresión polinomial tiene más de tres términos simplemente se le llama polinomio, aunque existen las denominaciones cuatrinomio, quintinomio pero son poco usadas.
Por el grado del polinomio se pueden clasificar en:
- Polinomio constante o cero: es aquel en el que todos sus coeficientes son igual a cero (0).
- Polinomio lineal: donde su mayor grado es 1. Para este caso todos los términos tienen grado 1 o exponente igual a 1.
- Polinomio cuadrático: es una expresión polinómica donde la variable o término de grado más alto es 2.
- Polinomio cúbico: es aquel polinomio cuyo término de mayor grado es igual a 3.
- Polinomio heterogéneo: es el polinomio que tiene sus términos, o al menos dos de ellos, de diferentes grados.
- Polinomio homogéneo: es aquel donde todos sus términos poseen el mismo grado.
Por comparación de expresiones polinomiales se pueden clasificar en:
- Polinomios iguales: dos polinomios son iguales cuando se verifica la igualdad término a término.
- Polinomios semejantes: dos polinomios son semejantes si poseen las mismas variables o parte literal, sin importa los coeficientes
Operaciones con polinomios
Las operaciones algebraicas básicas se pueden realizar con los polinomios de diferentes tipos. Estas cuatro operaciones básicas sobre polinomios se pueden dar como:
Suma
- Artículo principal: Suma de polinomios.
Cuando se trata de la suma de polinomios, es necesario reunir los términos semejantes y luego sumarlos, respetando sus signos y se conserva la parte literal tal como está.
La suma se puede realizar de manera vertical, ordenando cada término semejante uno debajo del otro. Para la suma de manera horizontal, si los polinomios están entre paréntesis se debe eliminar realizando las operaciones de signo de ser necesarias, luego se suman los monomios semejantes.
Por ejemplo: la suma de los dos polinomios P(x) = 2y³ + 3y − 2, Q(x) = 2y − 2y² + 1y³ da como resultado 3y³ + 5y − 2 − 2y².
Resta
- Artículo principal: Resta de polinomios.
También se puede realizar de manera vertical o horizontal como en la suma, pero en este caso, simplemente se suma el inverso aditivo del polinomio que se está restando al otro polinomio. Por ejemplo. 2x3 + 5x2 -3x + 1 – (6x3 – 2x – 8).
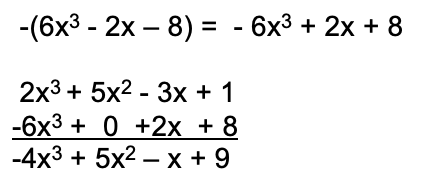 |
Los pasos para resolver una resta de polinomios son:
|
Multiplicación
- Artículo principal: Multiplicación de polinomios.
Esta operación matemática cumple con las propiedades distributiva, conmutativa y asociativa, por lo que, para resolver una multiplicación se aplican las propiedades necesarias, la regla de los signos y la regla de los exponentes y simplemente se multiplica cada término de un polinomio con cada término del otro polinomio y se simplifica de ser necesario.
Por ejemplo: la multiplicación de los dos polinomios P(x) = 2y³ + 3y − 2, Q(x) = 2y − 2y² + 1y³ da como resultado .
División
- Artículo principal: División de polinomios.
Para la división se toma en cuenta la regla de los signos de la potenciación. Así, para polinomio se dividen los coeficientes, y luego las variables según la ley de exponentes (se restan los exponentes).
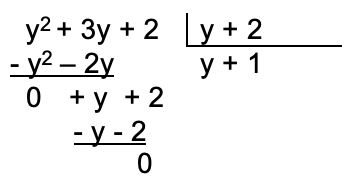 |
Los pasos para resolver una división de polinomios son:
|
Ejemplos
Algunos ejemplos de polinomios son:
| 3x3 – 4x – 5 | 7y – 11xy – 3x | 2y2 – 2y – 1 |
| -3x3 + 2x2 + 5y | 2x3 – 7y + 2 | 2x2 + 6y – 14 |
| 6x2 + 2x – 3 | 2x + 3x2 – 2x³ | 2x3 + 6x + 5 |
| 4y2 + 2y – 4 | 15x3 – 1y + 1 | x2 + 3y – 7 |
Ejercicios resueltos
Ejercicio #1
Problema a resolver: clasifica los siguientes polinomios según lo estudiado:
| Expresión polinomial | Solución |
| -6x3 + 4x2 + 3x – 5 | |
| P(x) = -x4 + 5xy2 – 6
L(x) = + 5xy2 – x4 – 6 |
|
| 4x2 + 2x + 5 | |
| 5m – 3n – 6 | |
| Q(mn)= 6m3n + 4mn – 1
R(mn) = -2m3n + mn – 6 |
Ver solución
| Expresión polinomial | Solución |
| -6x3 + 4x2 + 3x – 5 | Polinomio (cuatrinomio) por tener 4 términos – Heterogéneo y cúbico (grado 3). |
| P(x) = -x4 + 5xy2 – 6
L(x) = + 5xy2 – x4 – 6 |
P(x) y L(x) son polinomios iguales, tienen los mismos términos. |
| 4x2 + 2x + 5 | Trinomio – cuadrático (es de grado 2). |
| 5m – 3n – 6 | Trinomio lineal |
| Q(mn)= 6m3n + 4mn – 1
R(mn) = -2m3n + mn – 6 |
Cada expresión polinomial es un trinomio y entre sí son semejantes, tiene la misma parte literal |
Ejercicio #2
Problema a resolver: dadas las expresiones polinomiales: P(m) = – m3 + 3m – 2 y Q(m) = 2m3 + 6m2 – 3m + 4, realizar la suma.
Ver solución
Se realizará la suma ordenando los polinomios de manera vertical.

P(m) + Q(m) = m3 + 6m2 + 2
Ejercicio #3
Problema a resolver: realizar la multiplicación de los siguientes polinomios (6x3 – 2x) * (7x2 – 3x)
Ver solución
Se aplica la propiedad distributiva, multiplicando cada término del primero polinomio por cada término del segundo polinomio.
(6x3 – 2x) * (7x2 – 3x) = (6x3 * 7x2) + (6x3 * (-3x)) + ((-2x) * 7x2) + ((-2x) * (-3x))
= 42x5 – 18x4 – 14x3 +6x2.
Por tanto, (6x3 – 2x) * (7x2 – 3x) = 42x5 – 18x4 – 14x3 +6x2.
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana