Contenidos
Cubo
Figura tridimensional perteneciente al grupo de los poliedros.
Definición
Un cubo es una figura tridimensional (3D) perteneciente al grupo de los poliedros. También se dice que es un hexaedro regular o prisma cuadrado. Es considerado una de las formas más simples en el espacio tridimensional.
El cubo se caracteriza por:
- Tiene 6 caras, 12 aristas y 8 vértices.
- Todas sus caras con cuadrados.
- Es uno de los cinco sólidos platónicos, es decir todas sus caras son polígonos regulares convexos y congruentes.
- Su largo, ancho y altura son iguales.
- Las aristas opuestas del cubo son paralelas entre sí.
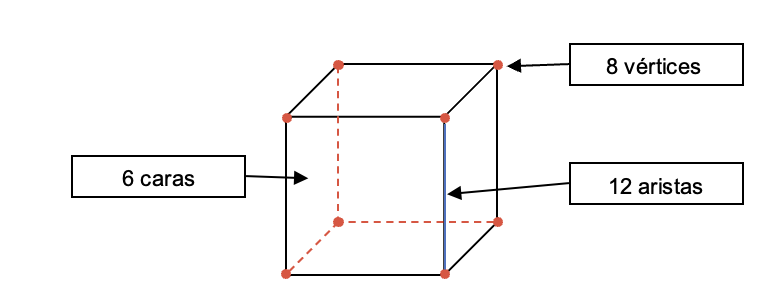
Elementos y partes
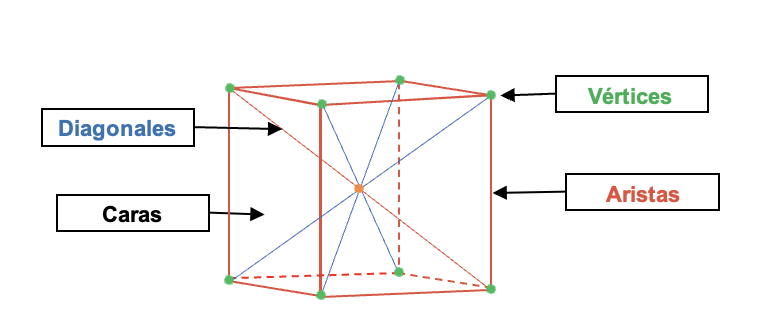
Los elementos del cubo se muestran en la figura de abajo y se describen a continuación:
- Caras: es cada uno de los polígonos que limita el cubo. Como se mencionó está formado por 6 cuadrados.
- Aristas: es la línea que se forma cuando se unen dos caras. Cada arista es un lado en común a dos caras consecutivas.
- Vértices: es el punto donde se unen las aristas correspondientes.
- Diagonal: es la línea que se traza desde un vértice hasta su opuesto de la cara que se encuentra al frente. En total se forman 4 diagonales.
- Ángulo diedro: se forma por la unión de dos caras.
- Ángulo poliedro: se forma por los lados que coinciden en un solo vértice.
Diagonales
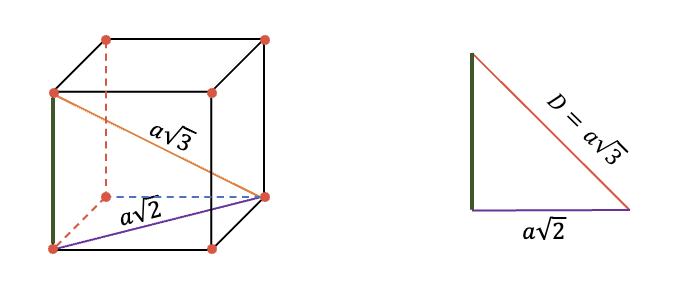
El cubo tiene cuatro diagonales y para hallar la longitud de cualquiera de estas se utiliza el teorema de Pitágoras. Cada cara diagonal forma la hipotenusa del triángulo rectángulo formado.
Entonces la diagonal viene dada por:
Publicidad, continua debajo- Longitud de la cara diagonal del cubo =
, donde «a» es la longitud de la cara del cubo.
- Longitud de la diagonal principal =
.
La diagonal es: .
Donde D es la diagonal y a es la longitud de la cara del cubo
Volumen
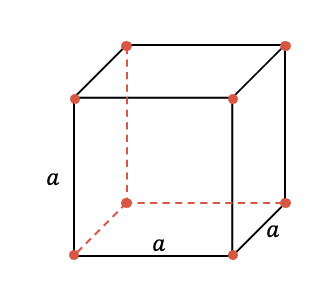
El volumen del cubo se calcula multiplicando el valor de la longitud de sus tres dimensiones, ancho, largo y altura.
Sin embargo, como cada una de las aristas o lados del cubo son de igual longitud, la fórmula del volumen del cubo será:
Donde: V es el volumen y a es la longitud del lado del cubo.
La unidad de medida del volumen viene dada en unidades cúbicas, centímetros cúbicos (cm3), metros cúbicos (m3), entre otras medidas de longitud.
Área
El área superficial del cubo resulta de sumar las áreas de cada una de las caras. Ahora bien, se sabe que el cubo está formado por cuadrados y que el área de un cuadrado es igual = a2 .
Entonces, el área de una de las caras se multiplica por 6 (número de caras del cubo), quedando la fórmula de la manera siguiente:
Donde a es el lado del cubo.
Otra manera de hallar el área del cubo es en función de la diagonal. Para este caso, se emplea la fórmula:
Donde: A es el área, D es la diagonal y a es la longitud del lado del cubo.
Ejercicios resueltos
Ejercicio #1
Problema a resolver: ¿Cuál es el área total de la superficie de un contenedor de agua, si el lado de cubo tiene una longitud de 4 metros?
Ver solución
La longitud de la arista o lado del cubo es de 4 metros, usando la fórmula:
Sustituyendo los valores
El área de superficie que ocupa el almacenador de agua es de 96 metros cuadrados.
Ejercicio #2
Problema a resolver: se tiene una caja de regalos que tiene forma de hexaedro regular, cuya longitud de su lado es de 12 centímetros. Hallar el volumen de la caja.
Ver solución
Para hallar el volumen se utiliza la fórmula:
Sustituyendo el valor del lado, se obtiene:
El volumen de la caja de regalo es de 1728 centímetros cúbicos.
Ejercicio #3
Problema a resolver: se tiene que la diagonal de un cubo es de 35 pulgadas, ¿Cuál es el área del cubo?
Ver solución
Como se conoce la diagonal del cubo, se utiliza la fórmula del área en función de la diagonal: .
Sustituyendo el valor de la diagonal:
El área del cubo conocida su diagonal es de 2450 pulgadas2
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana