Esfera

Definición

Una esfera es una figura geométrica tridimensional de forma redonda.

Es definida como un cuerpo redondo que se genera al girar el semicírculo de radio alrededor de su diámetro .

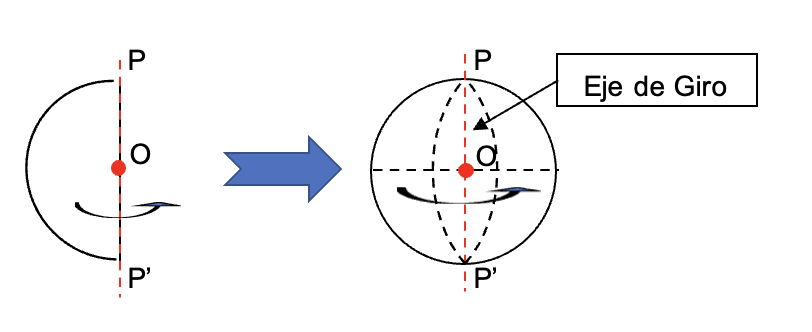
Este tipo de figuras se distinguen por no tener caras planas, ni vértices, ni bordes, sino superficies curvas y los puntos en su superficie son equidistantes del centro.

Por lo tanto, la distancia entre el centro y la superficie de la esfera es igual en cualquier punto, que es lo que se conoce como el radio de la esfera.

Desde una perspectiva matemática, la esfera es una combinación de un conjunto de puntos conectados con un punto común a distancias iguales en tres dimensiones.

Características

Propiedades de una esfera Las esferas poseen las siguientes propiedades que permiten identificarla fácilmente. Estas propiedades también se denominan atributos de la esfera.

• Una esfera se define en tres dimensiones, es decir, eje x, eje y y eje z.
• Es un objeto simétrico en todas las direcciones.
• Todos los puntos de la superficie equidistan del centro.
• Una esfera tiene solo una superficie curva, no es un poliedro porque no tiene vértices, aristas ni caras planas.
• La curvatura de la superficie permanece igual a lo largo de toda la superficie.
• La sección transversal de una esfera tiene forma circular. Esto significa que una representación bidimensional de una esfera es un círculo cuando solo se dispone de dos ejes.
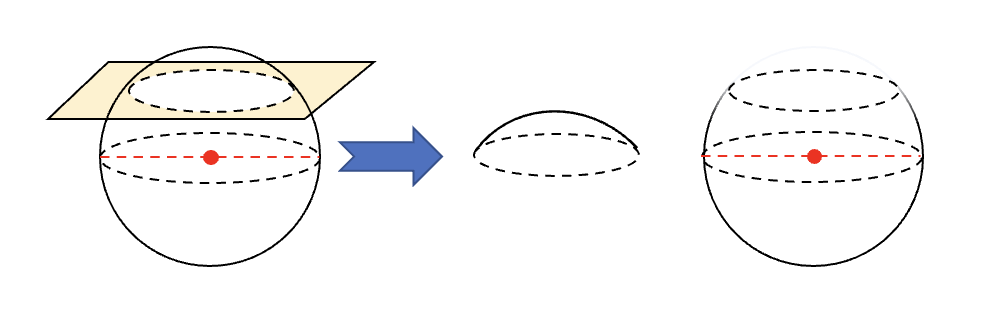
• Al cortar una esfera por un plano resultan dos casquetes esféricos.

Elementos y partes

Los elementos más importantes de una esfera son los siguientes:

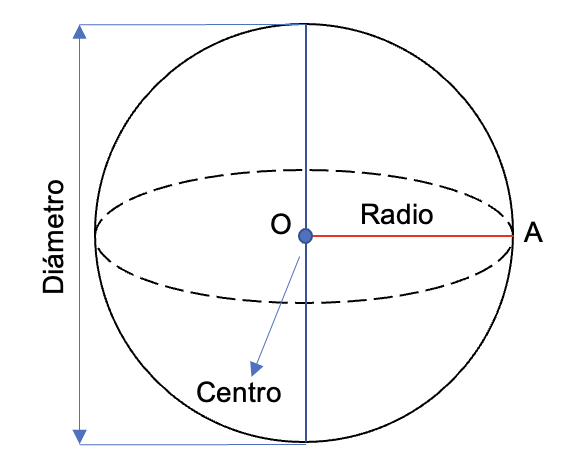
• Radio: la longitud del segmento de línea trazado entre el centro de la esfera y cualquier punto de su superficie. En la figura de ejemplo, se tiene que “O” es el centro de la esfera y “A” es cualquier punto en su superficie, entonces la distancia OA es su radio.
• Circunferencia: la longitud del gran círculo de la esfera se llama su circunferencia. En la figura del ejemplo, el límite del círculo punteado o la sección transversal de la esfera que contiene su centro se conoce como su circunferencia.
• Volumen: es la cantidad de espacio ocupado por la esfera se conoce como el volumen y se expresa en unidades cúbicas.

Volumen

La fórmula de la esfera para el volumen se expresa mediante la siguiente ecuación: En la fórmula el radio se encuentra elevado al cubo. Esto se debe a que el volumen representa el espacio en tres dimensiones.

Donde:

• V = es el volumen de la esfera
• p = es una constante aproximadamente de 3,1416
• r = es el radio de la esfera

El volumen de la esfera depende del radio de la esfera, por lo tanto, al variar su medida cambia el volumen de la esfera.

Debido a esto, las unidades de volumen siempre se representan como unidades cúbicas. Las unidades de volumen métricas son metros cúbicos o centímetros cúbicos, pulgadas cúbicas o pies cúbicos.

Los pasos para calcular el volumen de una esfera son:

1. Paso 1: Comprobar el valor del radio de la esfera.
2. Paso 2: Hallar el cubo del radio.
3. Paso 3: Multiplicar el valor obtenido del radio por .

Otras fórmulas de la esfera que son importantes conocer y que pueden ser utilizadas como pasos intermedios para hallar el volumen son:

• Diámetro: que se define como una cuerda que pasa por el centro de la circunferencia. El diámetro es el doble del radio. D = 2r. En función del volumen
• Circunferencia: .

Ejercicios resueltos

Ejercicio #1

Problema a resolver: se tiene una esfera cuyo radio es de 9 cm. Hallar el espacio que ocupa la esfera.

Ejercicio #2

Problema a resolver: hallar el volumen de una esfera cuyo diámetro es de 12 centímetros.