Contenidos

Inicio / Matemática / Geometría / Área de un cuadrado

Matemática

Geometría

Área de un cuadrado

Medida de la superficie de un cuadrado, espacio que ocupa en el plano bidimensional.

Por

Haude Medina

Tabla de contenidos:

Definición

El área de un cuadrado es la medida de su superficie, es el espacio que ocupa en el plano bidimensional.

Una manera sencilla de comprender la definición del área del cuadrado es conociendo el número de unidades cuadradas necesarias para llenar completamente un cuadrado.

Por ejemplo, se tiene un tablero, el cual está dividido en sus lados en 8 partes iguales, como se muestra en la figura.

Se puede observar, que se forman un total de 64 cuadros para rellenar el cuadrado completamente, si cada cuadro se considera mide 1 unidad, entonces el área del cuadrado es igual a 64 unidades².

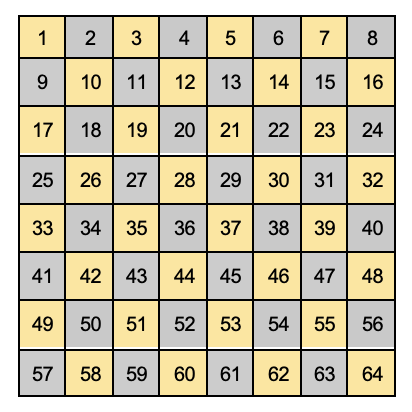
Área de un cuadrado

Ahora bien, en vez de contar todos los cuadros formados, se puede multiplicar la cantidad de cuadros de dos de sus lados 8 x 8 y esto da como resultado 64.

Así se puede decir, que el área es la cantidad de cuadros de cierta medida que caben dentro del cuadrado.

Publicidad, continua debajo

La medida de superficie del cuadrado se expresa en unidades cuadradas, por ejemplo, metros cuadrados (m²), centímetros cuadrados (cm²), pulgadas cuadradas (in²), entre otras medidas de longitud, pero siempre expresadas al cuadrado.

Cálculo

Área del cuadrado conocida la medida de sus lados

La manera más conocida para hallar el área del cuadrado, es utilizando la fórmula general del área de un paralelogramo:

$A=b\ast h\$

donde «A» corresponde al área, «b» es la base y «h» la altura.

Área de un cuadrado

Por ser el cuadrado un paralelogramo con todos sus lados congruentes, la fórmula anterior se simplifica de la siguiente manera:

$A=b\ast h\ \rightarrow A=l\ast l$

$A=l^2$

siendo «l» el lado del cuadrado. Así, tan sólo es necesario conocer un lado del cuadrado para poder hallar su área.

Área del cuadrado en función de las diagonales

Otra manera de hallar el área del cuadrado, es en función de su diagonal, para esto se aplica la fórmula: $A=\frac{D^2}{2}$ .

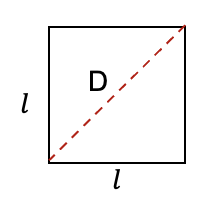
Área de un cuadrado

En el cuadrado «l» es la medida de los lados y “D” es la diagonal, la cual divide el cuadrado en dos triángulos rectángulos congruentes. Aplicando el teorema de Pitágoras, se tiene que los lados «l» son los catetos y la diagonal es la hipotenusa.

${hipotenusa}^2={cateto}^2+{cateto}^2$

$D^2=l^2+l^2=2l^2$

$\frac{D^2}{2}=l^2$

Como $A=l^2,\ se\ tiene\ \rightarrow A=\frac{D^2}{2}$

Ejercicios resueltos

Ejercicio #1

Problema a resolver: un campo de juego tiene la forma de un cuadrado. Si uno de sus lados mide 3 metros, ¿cuál es la medida de su área?

Ver solución

Por ser un cuadrado todos sus lados son de igual medida, es decir cada uno mide 3 metros.

Aplicando la fórmula del área en función de la medida de los lados se tiene:

$A=l^2\rightarrow A=3^2$

$A=9{\ m}^2$

El área es de 9 metros cuadrados.

Ejercicio #2

Problema a resolver: se tiene una mesa cuadrada cuya diagonal es 60 pulgadas. Hallar la medida de sus lados y el área.

Ver solución

Conocida la diagonal de la mesa se puede utilizar la fórmula $\frac{D^2}{2}=l^2$ , para encontrar la medida de los lados.

$\frac{D^2}{2}=l^2\rightarrow\frac{\sqrt{D^2}}{\sqrt2}=\sqrt{l^2}$ , aplicando propiedad de radicales

$l=\frac{D}{\sqrt2}=\frac{60}{\sqrt2}=42,6\ pulgadas$

Cada lado de la mesa mide aproximadamente 42,6 pulgadas.

Ahora el área es:

$A=\frac{D^2}{2}=\frac{{60}^2}{2}=\frac{3600}{2}=1800\ {pulgadas}^2$

Ejercicio #3

Problema a resolver: se conoce que el área de un cuadrado es de 49 pies2 y se desean conocer cuanto miden sus lados.

Ver solución

$A=l^2$ $Despejando\ \ \ \ \ \ l=\sqrt A$ $l=\sqrt{49}=7pies$

Los lados del cuadrado miden 7 pies.

Bibliografía:
Matemáticas para 1.er curso de ESO. (2016). Santillana. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Área de un cuadrado. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/area-de-un-cuadrado/). Última edición: mayo 2024. Consultado el 20 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!