Contenidos

Inicio / Historia y Sociedad / Números racionales

Matemática

Álgebra

Números racionales

Número que puede expresarse en forma de fracción.

Por

Haude Medina

Tabla de contenidos:

Definición

Se define un número racional como aquel número que puede expresarse en forma de fracción. Toma la forma $\frac{a}{b}$ , donde el numerador “a” y el denominador “b” son números enteros $(\mathbb{Z}),\$ y b > 0.

El conjunto de los números racionales se denota con la letra $\mathbb{Q}$ y, a este conjunto pertenecen el conjunto de los números naturales ( $\mathbb{N}$ ) y enteros ( $\mathbb{Z}$ ). Donde, $\mathbb{N}\in \mathbb{Z}\in\mathbb{Q}$ . La relación de pertenencia se muestra en la figura a continuación:

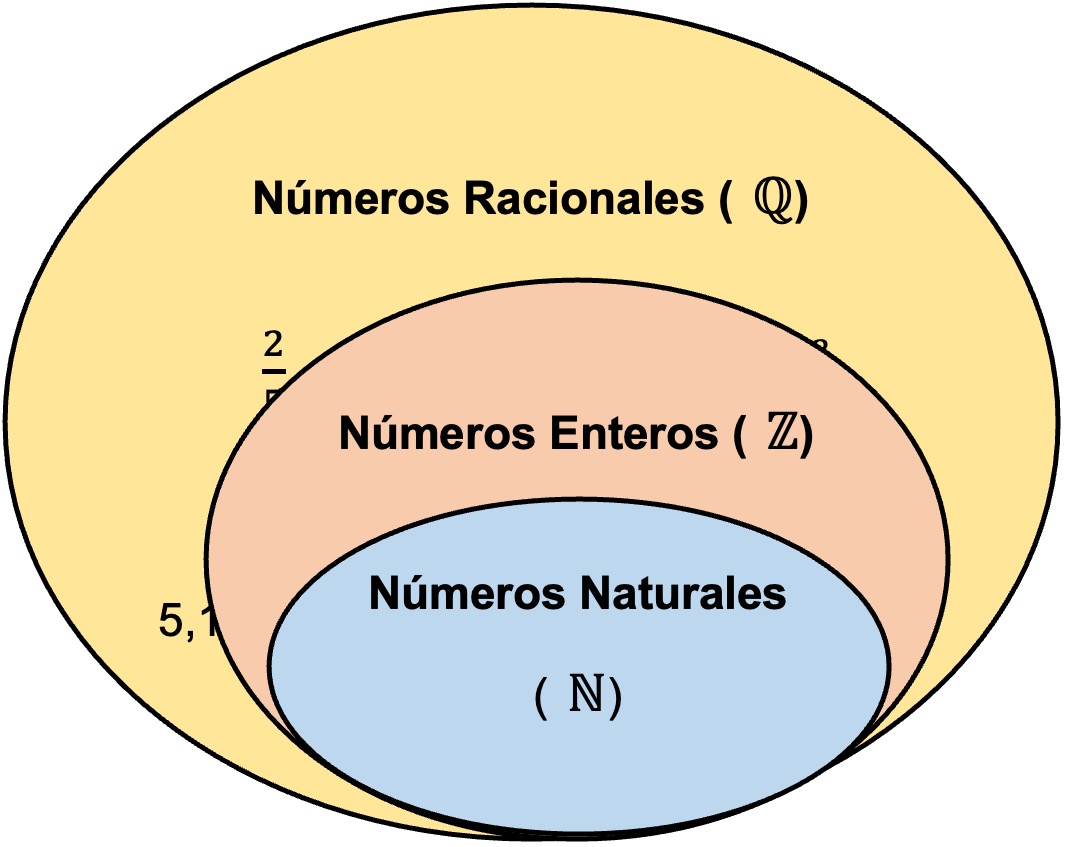
Conjunto de números racionales.

Los números racionales se pueden escribir como un número decimal, el cual resulta de dividir el numerador de la fracción entre el denominador. Dependiendo de la parte decimal, pueden distinguirse tres tipos:

Decimal exacto: se caracteriza por tener una parte decimal finita, $\frac{9}{15}$ = 0,6.
Decimal periódico puro: en la que su parte decimal se repite indefinidamente (período) inmediatamente después de la coma (,). Ejemplo $\frac{13}{3}$ = 4,33333.
Decimal periódico mixto: es aquel en la que el
periodo no está enseguida de la coma. Ejemplo $\frac{1}{15}$ = 0,02222.

Por otra parte, para determinar si el signo de un número racional fraccionario es (+) o (-), se deben considerar los signos del numerador y del denominador. Si estos son iguales, el racional es positivo (+), de ser diferentes; el racional es negativo (-). Esto se da por la ley de los signos.

Considerando las fracciones $\frac{3}{4}$ y $\frac{-4}{-15}$ , ambas son positivas por tener el mismo signo, para el caso de $\frac{-4}{-15}$ se puede escribir como $\frac{4}{15}$ .

En cambio, para las fracciones $\frac{-2}{7}$ y $\frac{8}{-9}$ , ambas son negativas por tener signos diferentes y se pueden escribir como: $-\frac{2}{7}$ y $-\frac{8}{9}$ .

Propiedades

El conjunto de los números racionales cumple con las propiedades clausurativa, conmutativa, asociativa, modulativa y distributiva para las operaciones de suma y multiplicación.

Publicidad, continua debajo

Clausurativa: el resultado, de una suma o de una multiplicación de dos o más números racionales, siempre es otro número racional. $\frac{a}{b}+\frac{c}{d}=\frac{e}{f}$ , donde $\frac{e}{f}\in\mathbb{Q}$ . Para la multiplicación $\frac{a}{b}\ast\frac{c}{d}=\frac{e}{f}$ , donde $\frac{e}{f}\in\mathbb{Q}$ .
Conmutativa: refiere que el orden en el cual se encuentren los sumandos o factores de una suma o multiplicación, respectivamente, no altera el resultado. Para la suma se cumple que $\frac{a}{b}+\frac{c}{d}=\frac{c}{d}+\frac{a}{b}$ . En cuanto a la multiplicación $\frac{a}{b}\ast\frac{c}{d}=\frac{c}{d}\ast\frac{a}{b}$ . A manera de ejemplo; en el caso de la suma: $\frac{3}{4}+\frac{5}{9}=\frac{5}{9}+\frac{3}{4}$ . Para el caso de la multiplicación $\frac{8}{9}\ast\frac{1}{3}=\frac{1}{3}\ast\frac{8}{9}$ .
Asociativa: la forma en que se agrupen los números racionales en la suma no afecta el resultado. $\frac{a}{b}+\left(\frac{c}{d}+\frac{g}{h}\right)=\left(\frac{a}{b}+\frac{c}{d}\right)+\frac{g}{h}$ . Por ejemplo $\frac{3}{5}+\left(\frac{5}{9}+\frac{1}{3}\right)=\left(\frac{3}{5}+\frac{5}{9}\right)+\frac{1}{3}$ . En el caso de la multiplicación la propiedad asociativa se expresa como: $\frac{a}{b}\ast\left(\frac{c}{d}\ast\frac{g}{h}\right)=\left(\frac{a}{b}\ast\frac{c}{d}\right)\ast\frac{g}{h}$ . Utilizando números sería: $\frac{1}{3}\ast\left(\frac{2}{5}\pm\frac{1}{4}\right)=\left(\frac{1}{3}\ast\frac{2}{5}\right)\pm\left(\frac{1}{3}\ast\frac{1}{4}\right)$ .
Distributiva: el producto de un número racional por una suma o resta de números racionales, es equivalente a la suma o resta de los productos del número racional por cada fracción. Se expresa como $\frac{a}{b}\ast\left(\frac{c}{d}\pm\frac{g}{h}\right)=\left(\frac{a}{b}\ast\frac{c}{d}\right)\pm\left(\frac{a}{b}\ast\frac{g}{h}\right)$ . Ejemplificando lo descrito: $\frac{1}{3}\ast\left(\frac{2}{5}\pm\frac{1}{4}\right)=\left(\frac{1}{3}\ast\frac{2}{5}\right)\pm\left(\frac{1}{3}\ast\frac{1}{4}\right)$ .
Elemento neutro o modulativa: para la suma el elemento neutro es el cero (0). A todo número racional que se le sume 0, el resultado es el mismo número racional. $\frac{a}{b}+0=\frac{a}{b}$ . En cambio, en el caso de la multiplicación el elemento neutro es el 1, por lo que $\frac{a}{b}\ast1=\frac{a}{b}$ .

Operaciones

Una vez explicado cómo está conformado el conjunto de los números racionales, dentro de este se pueden definir las operaciones básicas fundamentales, suma, resta, multiplicación y división para números fraccionarios.

Suma y resta de números fraccionarios

Para la suma o resta de números fraccionarios existen dos casos, cuando los denominadores son iguales o cuando los denominadores son diferentes.

En el caso de fracciones de igual denominador, se coloca el mismo denominador y se suman o restan los numeradores, dependiendo del caso. Supóngase las siguientes operaciones:

Suma	Resta
$\frac{3}{4}+\frac{5}{4}+\frac{1}{4}=\frac{3+5+1}{4}=\frac{9}{4}$	$\frac{11}{3}-\frac{4}{3}=\frac{11-4}{3}=\frac{7}{3}$

Cuando se tienen fracciones con diferente denominador, se deben hallar fracciones equivalentes, con igual denominador, a los números racionales dados. Luego se suman o restan las fracciones equivalentes obtenidas, por el método de multiplicación cruzada o m.c.m.

Suma	Resta
$\frac{9}{7}+\frac{1}{4}=\frac{\left(9\ast4\right)+\left(7\ast1\right)}{7\ast4}$ $=\frac{36+7}{28}=\frac{43}{28}$	$\frac{3}{5}-\frac{2}{9}=\frac{\left(3\ast9\right)-\left(2\ast5\right)}{5\ast9}$ $=\frac{27-10}{45}=\frac{17}{45}$

Suma

Resta

$\frac{9}{7}+\frac{1}{4}=\frac{\left(9\ast4\right)+\left(7\ast1\right)}{7\ast4}$

$=\frac{36+7}{28}=\frac{43}{28}$

$\frac{3}{5}-\frac{2}{9}=\frac{\left(3\ast9\right)-\left(2\ast5\right)}{5\ast9}$

$=\frac{27-10}{45}=\frac{17}{45}$

Encuentra más información de la suma de fracciones y resta de fracciones.

Multiplicación de fraccionarios

Se expresa como $\frac{a}{b}\ast\frac{c}{d}=\ \frac{a\ast c}{b\ast d}$ . Por ejemplo, si se desea hallar el producto de las fracciones:

$\frac{10}{3}\ast\frac{1}{6}=\frac{10\ast1}{3\ast6}=\frac{10}{18}$ , simplificando, $\frac{5}{9}$

Encuentra más información sobre la multiplicación de fracciones.

División de fraccionarios

Se define el cociente o división de dos fraccionarios como: $\frac{a}{b}\div\frac{c}{d}=\frac{a\ast b}{b\ast c}$ .

Por ejemplo, llevándolo a números:

$\frac{5}{9}\ast\frac{3}{8}=\frac{5\ast8}{9\ast3}=\frac{40}{27}$

Encuentre más información sobre la división de fracciones.

Ejemplos

Algunos ejemplos de números racionales son:

1	-8	$\frac{15}{2}$	$\frac{29}{42}$
$1\frac{10}{3}$	0.25	10	$\frac{1}{7}$
3	$-\frac{5}{6}$	1.50	$\frac{2}{9}$
$\frac{16}{5}$	-6	$\frac{45}{25}$	33

Bibliografía:
Matemáticas para 1.er curso de ESO. (2016). Santillana. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador. Ministerio de Educación del Ecuador. (2016). Matemática 9° grado. Libro del estudiante. SMEcuaediciones.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Números racionales. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/numeros-racionales/). Última edición: marzo 2022. Consultado el 20 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!