Contenidos

Inicio / Matemática / Álgebra / Números complejos

Matemática

Álgebra

Números complejos

Combinación de un número real y un número imaginario.

Por

Haude Medina

Tabla de contenidos:

Definición

El conjunto de los números complejos se forma de la combinación de un número real y un número imaginario y se denotan con la letra $\mathbb{C}$ . En términos de conjuntos: $\mathbb{N}\subset\mathbb{Z}\subset\mathbb{Q}\subset\mathbb{R}\subset\mathbb{C}$ .

Quiere decir, que se puede definir este conjunto de números, como aquellos que se escriben en la forma a + b · i, donde a y b son números reales. Por lo general, se omite el punto y se escribe de la forma a + bi.

De esto, se pueden distinguir los elementos de un número complejo que son: una parte real (el número que no acompaña a “i”) sumado a una parte imaginaria que corresponde al número que acompaña a “i”.

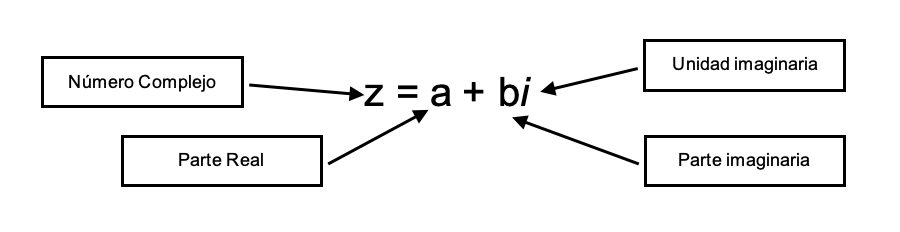
Elementos de un número complejo

Los números complejos escritos de la forma anterior, que es la más común encontrar, están escritos en forma binómica, donde la letra “z” expresa que es un número complejo y se distinguen la parte real y la parte imaginaria. Son ejemplos de números complejos: $z=2\ +\ 3i,\ \ \ z=\frac{3}{4}+6i$ .

También se puede decir que en un número real su parte imaginaria es 0, por ejemplo, para $z\ =\ 5\ +\ 0i$ , se tiene que $0i\ =\ 0$ , por lo que $z\ =\ 5$ , un número real.

Otro caso, es el conocido como un número imaginario puro que es de la forma $z\ =\ 0\ +\ 2i\ \ =\ 2i$ , la parte real es 0 y solo tiene la parte imaginaria.

Publicidad, continua debajo

De esta manera, se pueden distinguir los números complejos expresados en forma binómica $z=2\ +\ 3i$ , los números complejos puramente reales $z\ =\ 5$ y los números complejos puramente imaginarios $z=\ 2i$ .

Estos números surgen para dar respuestas a las raíces negativas, que en el conjunto de los Reales no tiene solución, por ejemplo; $\sqrt{-4}$ no tiene solución conocida en $\mathbb{R}$ , por tanto $\sqrt{-4}=\sqrt4\ast\sqrt{-1}=2i$ .

Propiedades

Las propiedades de los números complejos se aplican en las operaciones de suma y multiplicación, estas son:

Propiedad de cierre o cerradura: al sumar o multiplicar dos o más números complejos el resultado que se obtiene también es un número complejo. Para la suma: $z_1,\ z_2\ \in\mathbb{C}$ , se tiene que $\ z_1+\ z_2\ \in\mathbb{C}$ . En la multiplicación $z_1,\ z_2\ \in\mathbb{C}$ , se tiene que $\ z_1\ast\ z_2\ \in\mathbb{C}$ .
Propiedad conmutativa: en la suma para cualesquiera $z_1,\ z_2\ \in\mathbb{C}$ , se cumple que $\ z_1+\ z_2=\ z_2+z_1$ . En el caso de la multiplicación: para cualesquiera $z_1,\ z_2\ \in\mathbb{C}$ , se cumple que $\ z_1\ast\ z_2=\ z_2\ast z_1$ .
Propiedad asociativa: en la suma esta propiedad se expresa como: siendo $z_1,\ z_2,\ z_3\ \in\mathbb{C}$ , se cumple que $z_1+\ z_2=\ z_2+z_1$ . En el caso de la multiplicación $z_1,\ z_2\ \in\mathbb{C}$ , se cumple que $\ \ {(z}_1\ast\ z_2)\ast z_3\ =\ z_1\ast{(z}_2\ast z_3)$ .
Inverso aditivo u opuesto (para la suma): todo número complejo z tiene un único inverso aditivo, denotado como -z, donde $z+\left(-z\right)=0$ . El opuesto de $z=a+bi\$ es el número complejo (-a –bi).
Propiedad distributiva: combina las operaciones de multiplicación con suma o resta, donde se tiene que para cualesquiera $z_1,\ z_2,\ z_3\ \in\mathbb{C}$ , se cumple que $\ z_1\ast\ {(z}_2\pm z_3)=z_1\ast z_2\pm z_1\ast z_3$ .

Se debe hacer notar que en la aplicación de las propiedades se conmuta, asocia, se halla el inverso del número complejo es su estructura completa, jamás se deben invertir las partes del número. Se utiliza para denotar el número complejo.

Operaciones con números complejos

Suma

Para sumar números complejos escritos de la forma binómica, se suman por separado las partes reales de las partes imaginarias. De manera general la suma de números complejos es:

$(a\ +\ bi)\ +\ (c\ +\ di)\ =\ (a\ +\ c)\ +\ (b\ +\ d)i$

Resta

La resta se realiza como cualquier binomio, combinando los términos semejantes y luego simplificar de ser posible. Para $z_1=\left(a\ +\ bi\right)\ y\ z_2=\ \left(c\ +\ di\right)$ , se tiene que:

${\ z}_1-\ z_2=\left(a\ +\ bi\right)-\ (c\ +\ di)\ =\ (a-\ c)\ +\ (b-\ d)i$

Multiplicación

Para la multiplicación se utiliza el método FOIL (primero, exterior, interior y último). Para obtener el producto de dos números complejos se multiplica cada elemento del primer número complejo por cada una de las partes del segundo número complejo, recordando las propiedades de los números imaginarios, la cual se empleará.

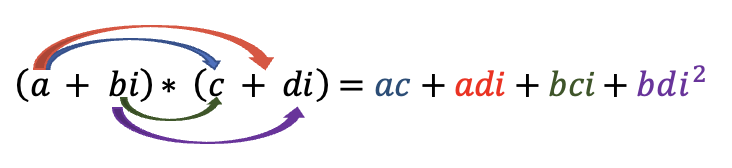
Multiplicación de números complejos.

El número $i^2=-1$ , por tanto $\ bdi^2=-bd$ , simplificando se tiene:

$\left(a\ +\ bi\right)\ast\ \left(c\ +\ di\right)=ac+adi+bci+bdi^2$

$=ac+adi+bci-bd$

$\left(a\ +\ bi\right)\ast\ \left(c\ +\ di\right)=\left(ac-bd\right)+\left(ad+bc\right)i$

División

Para la división de números complejos, primero se debe hallar el conjugado del número complejo del denominador o lo que es el divisor.

El conjugado de un número complejo se obtiene cambiando el signo de la parte imaginaria, $z=\left(a+bi\right)\rightarrow\bar{z}=(a-bi)$ .

Luego para realizar la división es preferible expresar en forma de fracción el dividendo y el divisor, para luego multiplicar tanto el numerador como el denominador por el conjugado hallado.

Dada la división $\frac{\left(a+bi\right)}{\left(c\ +\ di\right)}$ , se halla la conjugada del denominador que es $\bar{z}=\left(c-\ di\right)$

$\frac{\left(a+bi\right)}{\left(c\ +\ di\right)}=\frac{\left(a+bi\right)}{\left(c\ +\ di\right)}\ast\frac{\left(c-\ di\right)}{\left(c-\ di\right)}$

$\frac{\left(a+bi\right)}{\left(c\ +\ di\right)}=\frac{\left(ac+bd\right)+\left(bc-ad\right)i}{c^2+d^2}$

Ejemplos

Algunos ejemplos de números complejos son:

3 + 2i	1 + 2i	12 – i	18 + i
22 + 2i	3 – 4i	8 + πi	55 + 9i
3 + 2i	9 + i	8 – 23i	17 + 5i

Ejercicios resueltos

Ejercicio #1

Problema a resolver: realizar la suma de complejos $\left(3-2i\right)+\left(-4+6i\right)$ y verificar que se cumple la propiedad conmutativa.

Ver solución

Al realizar la suma de los números complejos dados, se debe considerar los signos negativos de algunas de sus partes y recordar la regla de signos.

Partiendo de la forma de suma estudiada:

$(a\ +\ bi)\ +\ (c\ +\ di)\ =\ (a\ +\ c)\ +\ (b\ +\ d)i$

$\left(3-2i\right)+\left(-4+6i\right)=(3+\left(-4\right)+\left(\left(-2\right)+6\right)i$

$=\left(3-4\right)+\left(-2+6\right)i$

$=-1+4i$

Aplicando la propiedad conmutativa se debe cumplir que:

$\left(3-2i\right)+\left(-4+6i\right)=\left(-4+6i\right)+\left(3-2i\right)$ . Desarrollando:

$\left(-4+6i\right)+\left(3-2i\right)=\left(\left(-4\right)+3\right)+\left(6+\left(-2\right)\right)i$

$=\left(-4+3\right)+\left(6-2\right)i$

$=-1+4i$

Se cumple la propiedad conmutativa

$\left(3-2i\right)+\left(-4+6i\right)=\left(-4+6i\right)+\left(3-2i\right)$

$-1+4i=-1+4i$

Ejercicio #2

Problema a resolver: desarrollar la división $(5+2i)\div(4+3i)$ .

Ver solución

primero se encuentra la conjugada del divisor $\left(4+3i\right)$ , su conjugada es $(4 - 3i)$ y se aplica la fórmula de la división:

$\frac{\left(a+bi\right)}{\left(c\ +\ di\right)}=\frac{\left(ac+bd\right)+\left(bc-ad\right)i}{c^2+d^2}$

Para visualizar mejor la división se expresa en forma de fracción

$\frac{\left(5+2i\right)}{\left(4+3i\right)}=\frac{\left(5+2i\right)}{\left(4+3i\right)}\ast\frac{\left(4-3i\right)}{\left(4-3i\right)}$

$=\frac{\left(5\left(4\right)+2\left(3\right)\right)+\left(2\left(4\right)-5\left(3\right)\right)i}{4^2+3^2}$

$=\frac{\left(20+6\right)+\left(8-15\right)i}{16+9}=\frac{26-7i}{25}$

Reescribiendo el resultado según la estructura de números imaginarios se obtiene que:

$\frac{\left(5+2i\right)}{\left(4+3i\right)}=\frac{26}{25}-\frac{7i}{25}$

Bibliografía:
Benavent, R. C. (abril 2016). Números reales y números complejos (Spanish Edition). Bubok Publishing. Francesca Pensieri, A. A. (1979). Números Complejos (2a ED.). Reverte.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Números complejos. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/numeros-complejos/). Última edición: mayo 2024. Consultado el 20 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!