Contenidos
Números decimales
Aquel número que tiene una parte entera y otra parte decimal.
Definición
Un número decimal es aquel que tiene una parte entera y otra parte decimal, ambas partes separadas por el separador decimal que puede ser un punto, una coma o un apóstrofo. El número decimal es una forma de escribir una fracción.
De esta definición, se distinguen tres partes fundamentales de un número decimal:
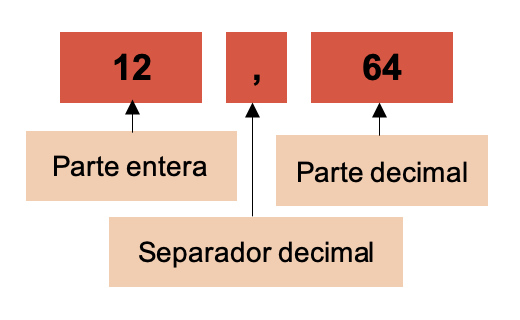
La parte entera siempre se ubica a la izquierda del separador decimal y la parte decimal se encuentra a la derecha del separador decimal.
Cada cifra de la parte decimal representa una fracción decimal, por tanto, los decimales son un valor entre 0 y 1, siendo números cuyo valor posicional se basan en potencias de 10 (la expresión 10ⁿ, donde n es un número entero).
A medida que la cifra del decimal se va alejando del separador decimal, el valor posicional de los dígitos se divide por 10 y mientras más lejos del separador decimal se encuentra será más pequeño.
Para comprender lo mencionado, se tomará como ejemplo el número decimal anterior 12,64 donde se tiene:
Publicidad, continua debajo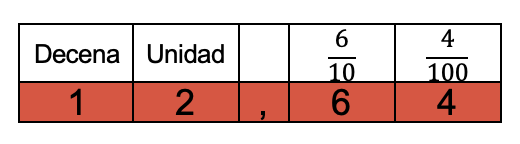
De esto, que la parte decimal también la nombran como parte fraccionaria y por tanto un número decimal se puede entender como una fracción decimal o como un número entero más una fracción decimal.
Valor posicional
Como se ha mencionado, cada dígito de la parte decimal ocupa una posición y dependiendo de esta tiene un valor. Para diferenciarlos, cada posición recibe un nombre, los cuales se muestran en la tabla a continuación:

Todos los valores posicionales de los decimales terminan es “ésimas” y no existe unésimas.
Una manera de nombrar la parte decimal es según el valor posicional, así, por ejemplo, el número decimal 12,64 se puede leer como doce y sesenta y cuatro centésimas.
También existen otras maneras de leerlo, como doce enteros y sesenta y cuatro centésimas. Otra forma sería, doce comas sesenta y cuatro centésimas.
Características
Los números decimales tienen diferentes características que se mencionan a continuación:
- El producto de dos números decimales siempre es el mismo, sin importar el orden en el que se multipliquen.
- Si un número entero y un número decimal se multiplican en cualquier orden, el producto sigue siendo el mismo.
- Si una fracción decimal se multiplica por 1, el producto es la propia fracción decimal.
- Si una fracción decimal se multiplica por 0, el producto es cero (0).
- Al dividir un número decimal por 1, el cociente es el mismo número decimal.
- Si un número decimal se divide por el mismo número, el cociente es 1.
- Si 0 se divide por cualquier decimal, el cociente es 0.
- La división de un número decimal por 0 no es posible, ya que el recíproco de 0 no existe.
Clasificación y tipos
Dependiendo de la parte decimal, pueden distinguirse cuatro tipos:
- Decimal exacto o finito: se caracteriza por tener una parte decimal finita, 0,342; 4,09; 127,5390192.
- Decimal infinito no periódico: si la parte decimal no se repite y existe una continuidad hacia el infinito. Por ejemplo π = 3,1415926535897932384626433832795…, su parte decimal es infinita y no sigue un patrón de repetición.
- Decimal periódico puro: su parte decimal se repite indefinidamente (período) inmediatamente después de la coma, por ejemplo; 3,12121212…
Para no escribir repetidamente la parte decimal y simplificar su escritura se coloca una línea horizontal sobre los decimales que se repiten,.
- Decimal periódico mixto: en este la parte periódica no está enseguida de la coma, por ejemplo; 0,12454545… Su escritura también se puede simplificar de la siguiente forma:
.
Operaciones con números decimales
En los números decimales es posible realizar cualquiera de las operaciones matemáticas básicas.
Suma de números decimales
La suma de decimales se realiza igual a una suma de enteros. Primero se deben colocar los sumandos en forma vertical, ordenando tanto la parte entera como la decimal según su valor posicional, uno debajo del otro, manteniendo el separador decimal intacto.
Se debe considerar que la parte entera se ordena posicionalmente antes del separador decimal, de derecha a izquierda, en cambio la parte decimal, se ordena después del separador decimal de izquierda a derecha. Ejemplo.

Resta de números decimales
El proceso de restar números decimales es similar a la resta de enteros, considerando el valor posicional de la parte entera y la parte decimal.
En los lugares donde la longitud de los números decimales no sea la misma se deben escribir ceros. Por ejemplo; realizar la resta: 147,37 – 75,751.
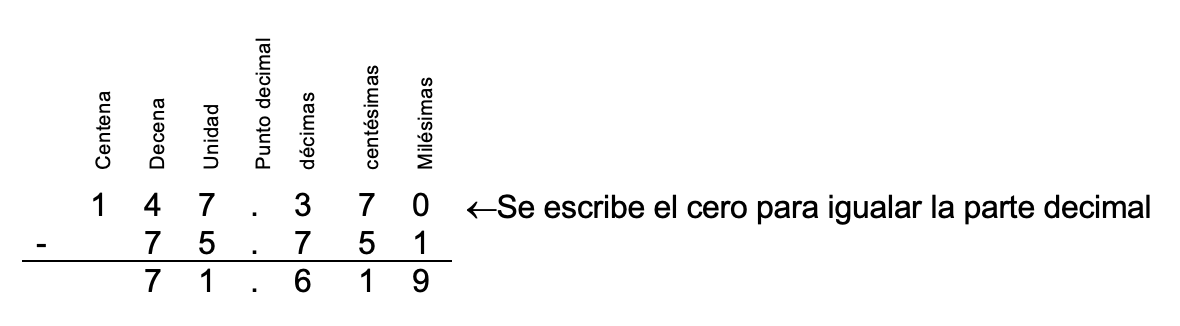
Multiplicación de números decimales
Para la multiplicación de números decimales se multiplican los números como enteros, es decir; como si no estuviese el separador decimal.
Una vez realizada la multiplicación, y en el resultado se corre la coma hacia la izquierda, tantas cifras decimales como tengan en total los dos factores.
División de números decimales
En la división de números decimales se pueden tener varios casos:
- División de un número decimal por un número entero, el proceso es el mismo como una división de números enteros, teniendo en cuenta las siguientes consideraciones: primero se dividen los dos números ignorando el punto decimal. Luego, el punto decimal en el cociente se coloca en la misma posición que en el dividendo. Por ejemplo, 248,2 ÷ 2 = 124,1.
- División de dos números decimales: existen varios métodos, el más sencillo es el siguiente,
Se multiplica el divisor por tantas decenas como sea necesario hasta obtener un número entero, y lo mismo se hace con el dividendo, pero por el mismo número de decenas. Luego se divide como números enteros. Por ejemplo: 45,6 ÷ 7,8.
45,6 se convierte en 456 y 7,8 se convierte en 78. Ahora se divide 456 ÷ 78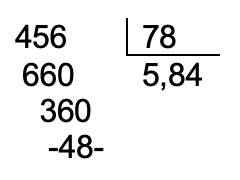
Ejemplos
Algunos ejemplos de números decimales son:
| 3,65 | 0,55 | 8,77 | 78,66 |
| 15553,01 | 1,99 | 43,44 | 25,05 |
| 18,09 | 15,55 | 11,23 | |
| 90,03 | 67,88 | 34,7 |
Ejercicios resueltos
Ejercicio #1
Problema a resolver: indicar cómo se leen los siguientes números decimales.
- 4,432
- 0,58
- 652,9023
Ver solución
a) 4,432
Solución: cuatro enteros y cuatrocientos treinta y dos milésimas.
b) 0,58
Solución: cincuenta y ocho centésimas. También se puede leer como cero coma cincuenta y ocho centésimas.
c) 652,9023
Solución: Seiscientos cincuenta y dos con nueve mil veintitrés diezmilésimos.
Ejercicio #2
Problema a resolver: en los siguientes números menciona que valor posicional tiene el dígito que se indica.
- 45,9786 valor posicional de 7.
- 1,396724 valor posicional del 4.
Ver solución
a) 45,9786 valor posicional de 7
Solución: El número 7 está a dos valores posicionales de la coma, lo que refiere que ocupa el lugar de las centésimas.
b) 1,396724 valor posicional del 4
Solución: El número 4 está a seis valores posicionales de la coma, por lo que ocupa el lugar de las millonésimas.
Ejercicio #3
Problema a resolver: resuelve la división 546,5 ÷ 5,25
Ver solución
Se multiplica el dividendo y el divisor por un mismo número, este número es la unidad seguida de tantos ceros (0) según la mayor cantidad de decimales que haya entre los dos números.
En este caso la mayor cantidad de decimales es dos del número decimal 5,25. Entonces:
546,5 * 100 = 54650, por su parte 5,25 * 10 = 525. Ahora se divide 54650 ÷ 525
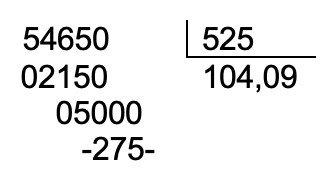
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.
 Enciclopedia Iberoamericana
Enciclopedia Iberoamericana