Contenidos

Inicio / Matemática / Geometría / Cono

Matemática

Geometría

Cono

Cuerpo geométrico que se genera al hacer girar un triángulo rectángulo alrededor de uno de sus catetos.

Por

Haude Medina

Tabla de contenidos:

Definición

Un cono es un cuerpo geométrico que se genera al hacer girar un triángulo rectángulo alrededor de uno de sus catetos. Tiene una base circular y se estrecha hasta un punto afilado llamado vértice.

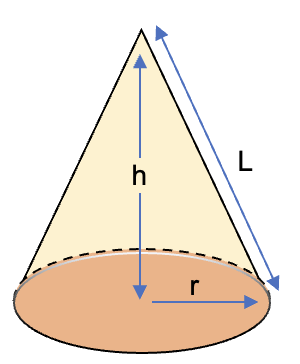
Imagen de un cono

También se puede definir el cono como una pirámide que posee una sección transversal circular, a diferencia de la pirámide que tiene una sección transversal triangular.

Propiedades

Entre las propiedades del cono se pueden mencionar:

El ángulo que forman la generatriz, en todas sus posiciones y el eje es constante.
Este tipo de figuras se distinguen por no tener caras planas, como un polígono, sino una superficie curva.
Un cono tiene una sola cara, que es la base circular pero no tiene aristas.
Un cono tiene un sólo vértice.
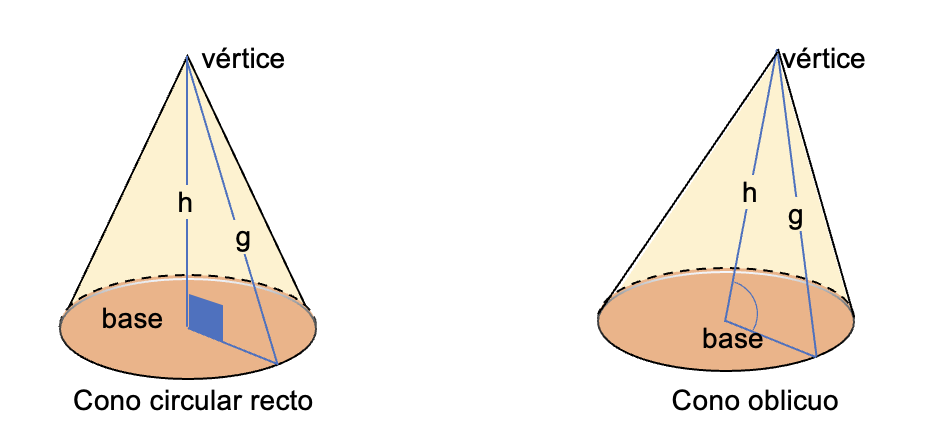
Se distinguen dos tipos, el cono circular recto y el cono oblicuo.
El cono circular recto está formado por una base circular y una línea recta unida al vértice superior.
En el cono circular recto el eje es perpendicular y va desde el vértice del cono hacia la base y pasa por el centro de la base circula.
El cono oblicuo tiene una base circular pero el eje del cono no es perpendicular a la base.
En el cono oblicuo el vértice de este no está ubicado directamente sobre el centro de su base circular.
La fórmula para la altura inclinada se obtiene utilizando el teorema de Pitágoras. La altura inclinada del cono es $\sqrt{(r^2\ +h^2\ )}$ .

Propiedades de un cono

Elementos y partes

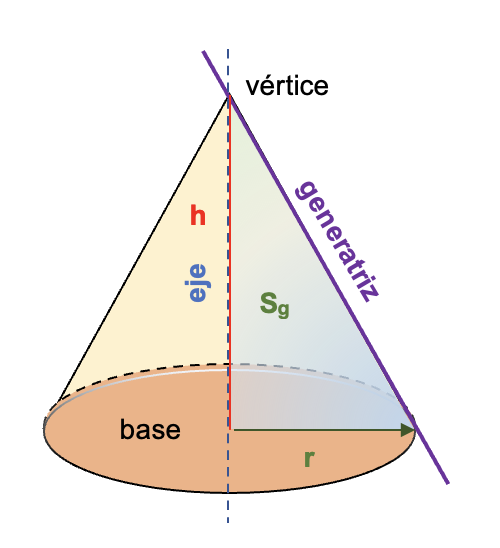
Los diferentes elementos del cono se describen a continuación y se representan de manera visual en la figura de abajo.

Base (B): es la cara plana inferior del cono sobre el cual se forma el cuerpo del cono. Esta es de forma circular.
Eje (E): Es una semirrecta imaginaria alrededor del cual gira el cateto del triángulo rectángulo que forma el cono. El eje coincide con la altura del cono.
Altura (h): es la distancia entre el vértice del cono y el centro de la base circular y coincide con el cateto alrededor del cual rota el triángulo para generar el cono.
Radio (r): es la distancia entre el centro de la base circular a cualquier punto de la circunferencia de la base. Por lo tanto, el diámetro del cono es la distancia a través de su base circular.
Vértice (V): punto donde confluyen las infinitas generatrices. Este es opuesto a la base circular.
Generatriz (g): son los segmentos de recta desde un punto de la circunferencia hasta el vértice superior.
Superficie generatriz (Sg): en el cono recto de revolución, es el triángulo rectángulo que lo origina al girar 360° sobre uno de sus catetos, que es el eje de rotación y, que es a su vez, la altura del cono. El otro cateto es el radio de la base. La hipotenusa es la generatriz (g).

Elementos y partes de un cono

Publicidad, continua debajo

Área y volumen

Área

Artículo principal: Área de un cono.

El área total de un cono resulta de la suma del área de la base (A_b) más el área del cuerpo de la figura o área lateral (A_L).

$A_t=\ A_b+A_l$

El área de la base es $A_b=\pi r^2$ mientras que el área de la superficie lateral se calcula multiplicando π por el radio de la base (r) y por la longitud de la generatriz (L) o (g), siendo $A_l=\ \pi\ast r\ast g$ .

Entonces, el área total del cono es:

$A_t=\left(\pi r^2\right)+\left(\pi\ast r\ast g\right)$

$A_t=\pi r(r+g)$

Se debe considerar que la generatriz es la hipotenusa del triángulo rectángulo que forma junto con el radio de la base y la altura del cono, siendo estos dos últimos los catetos.

$L=\sqrt{(r^2\ +h^2\ )}$

Volumen

El volumen es la medida equivalente a un tercio del producto entre el área de la base y la altura.

$V=\frac{1}{3}\pi r^2h$

Dónde:

V: es el volumen
π: es el número pi
r: es el radio
h: es la altura

Como en toda figura tridimensional el volumen está expresado en unidades cúbicas.

Ejercicios resueltos

Ejercicio #1

Hallar el volumen del cono circular recto que tiene una altura de 15 pulgadas y un radio de 8 pulgadas.

Ver solución

Se sabe que la fórmula para hallar el volumen del cono es $V=\frac{1}{3}\pi r^2h$ . Sustituyendo los valores conocidos se tiene que el volumen es:

$V=\frac{1}{3}\left(3,1416\right)\left(8^2\right)\left(15\right)=\frac{3016}{3}$

$V=1005,3\ {pulgadas\ }^3$

El volumen del cono es de 1005,3 pulgadas³.

Ejercicio #2

Calcular el área total de un cono que posee un radio de 14 cm y una altura de 20 cm.

Ver solución

El área total de un cono es $A_t=\pi r(r+g)$ . Para aplicar la fórmula primero se debe hallar la longitud de la generatriz o altura inclinada.

$L=\sqrt{r^2\ +h^2}=\sqrt{{14}^2\ +{20}^2\ }$

$L=\sqrt{196+400}=\sqrt{596}\rightarrow L=24,4\ cm (Altura inclinada)$

Aplicando la fórmula del área total.

$A_t=\left(3,1416\right)\left(14\right)\left(14+24,4\right)=43,9\left(38,4\right)$

$A_t=1685\ {cm}^2$

El área total es de aproximadamente 1685 cm².

Bibliografía:
Bruño, G.M. (s/f ). Elementos de la Geometría. Editorial Bouret. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador. Siu Kochoy, R., & Andaluz, C. (2019). Geometría del espacio: ejercicios y problemas. Fondo Editorial Universidad del Pacífico.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Cono. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/cono/). Última edición: mayo 2024. Consultado el 18 de mayo de 2024.

Copiar cita

¡Cita copiada a portapapeles!