Eneágono

Definición

Un eneágono es una figura geométrica plana que tiene nueve lados e igual número de vértices y ángulos.

Este polígono también recibe el nombre de nonágono, palabra que se deriva del latín “nonus” y “gon” que significan nueve lados.

Los lados del eneágono pueden ser de igual o diferente longitud al igual que sus ángulos y como en todo polígono, esto permite clasificarlos en varios tipos.

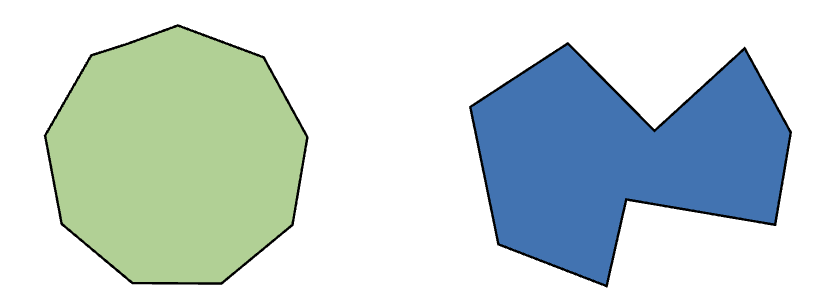
Las figuras mostradas son tipos de eneágonos donde se observa que sus lados pueden ser congruentes o no, al igual que sus ángulos.

Propiedades y características

A continuación, se describen una serie de características y propiedades que tienen los eneágonos.

• Los lados de un eneágono son estrictamente líneas rectas y no se pueden curvar.
• Un ángulo interior y exterior que comparten el mismo vértice suman 180°:
• La suma de los ángulos internos de cualquier eneágono es siempre 1260°. Dado que: Suma de ∠ = (n – 2) *180°, = (9 – 2) * 180° = 7 * 180° = 1260°.
• La suma de los ángulos externos de un eneágono cualquiera es de 360°.
• Este polígono tiene un total de 27 diagonales que se verifica con la fórmula
• De cada vértice del eneágono parten o concurren 6 diagonales.
• Las 6 diagonales que parten de un mismo vértice dividen al eneágono lo dividen siete triángulos, como se muestra en la figura.
• Un eneágono tiene 9 ejes de simetría.

Eneágono regular

Un eneágono regular se caracteriza por tener sus lados congruentes.

Todos los ángulos internos son iguales, cada uno con una amplitud de 140° que suman en total 1260°, mientras que sus ángulos externos cada uno mide 40°.

Apotema de un eneágono regular

En un eneágono regular su apotema se puede hallar como se indica a continuación, considerando los datos proporcionados en la figura siguiente

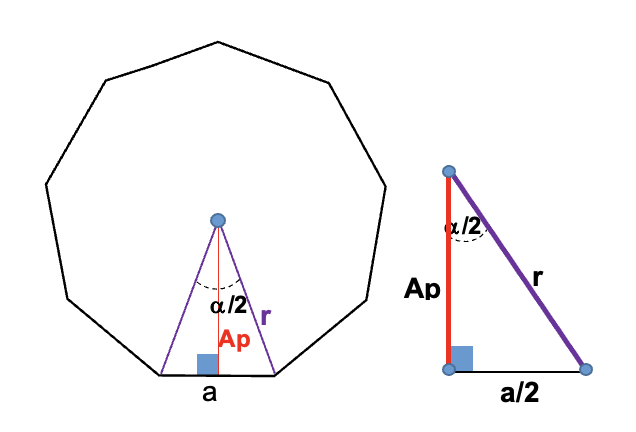
La intersección entre la apotema y el lado del polígono se forma un ángulo recto, por lo que es posible expresar la apotema como una función de la longitud del lado de la figura.

Donde “a” en la medida del eneágono.

También se puede emplear la fórmula:

Eneágono irregular

Se considera que un eneágono es irregular cuando al menos uno de sus lados tiene diferente longitud. Debido a esta característica, sus ángulos también son de diferente amplitud.

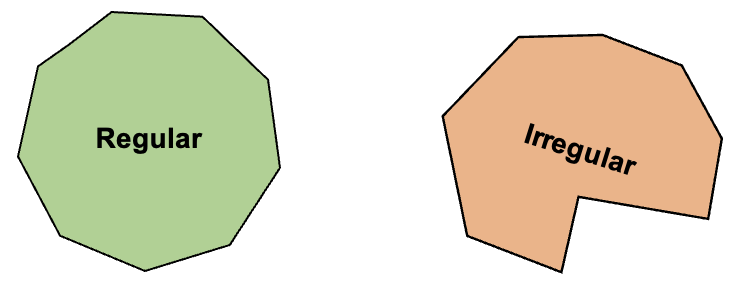
Además, de los tipos de eneágonos regulares e irregulares, este tipo de polígonos se puede clasificar según sus ángulos como convexos y cóncavos.

• Convexo: En este tipo de figura todos sus ángulos interiores miden menos de 180°. Todos los vértices apuntan hacia afuera.
• Cóncavo: Al menos uno de sus ángulos interiores debe ser mayor a 180°, con uno de sus ángulos apuntando hacia adentro.

Perímetro

El perímetro de un eneágono, como en todos los polígonos, resulta de sumar la longitud de cada uno de sus lados.

Donde {«a}_n» es la medida de cada uno de los lados.

Para los eneágonos regulares la fórmula se simplifica de la forma siguiente:

Área

Cuando se trata de un eneágono regular es posible calcular su área utilizando la fórmula:

Donde:

• A: es el área de la figura geométrica
• n: es el número de lados
• a: la longitud de uno de sus lados
• A_p: la apotema

Se puede simplificar la fórmula y hallar el área en función del perímetro conociendo que P = 9 * a, quedando:

Ejercicios resueltos

Ejemplo #1

Halle el perímetro de un eneágono regular con longitud de sus lados de 7 pulgadas.

Ejemplo #2

La medida de un lado de un eneágono regular es de 5 centímetros. ¿Cuál será el área de la figura?