Enciclopedia Iberoamericana
Contenidos
Rectángulo
Figura geométrica plana que se clasifica dentro de los paralelogramos.
Definición
El rectángulo es una figura geométrica plana que se clasifica dentro de los paralelogramos, por tener sus lados opuestos paralelos dos a dos y de igual longitud y además sus cuatro ángulos internos con medida de 90° cada uno.
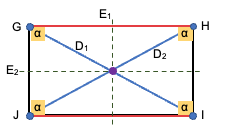
El rectángulo por ser del tipo paralelogramo adquiere los mismos elementos de este:
- Lados: son los cuatro segmentos de recta que forman el rectángulo:
,
,
,
.
- Vértices: es el punto donde se unen dos lados consecutivos, indicándose con las letras G, H, I, J.
- Ángulos: son cuatro ángulos internos (α), los cuales los opuestos entre sí, son de igual amplitud.
- Diagonales: es el segmento de recta que va desde un vértice hasta su vértice opuesto. El rectángulo tiene dos diagonales D₁,D₂.
- Ejes de simetría: se forman dos ejes de simetría E₁, E₂. Los cuales dividen al rectángulo en dos partes iguales con respecto a dicho eje.
Características
El rectángulo tiene características que adopta de los paralelogramos, más, sin embargo, tiene unas propias que lo diferencian del resto de los paralelogramos.
- Son figuras geométricas bidimensionales, por lo que solo tienen ancho y alto.
- Es un cuadrilátero por tener cuatro lados y un paralelogramo porque sus lados opuestos son paralelos.
- Son equiángulos debido a que sus cuatro ángulos internos tienen igual amplitud.
- Sus ángulos internos opuestos son congruentes y los ángulos consecutivos son suplementarios.
- Los lados opuestos entre sí tienen la misma medida
y
, mientras que los consecutivos son de diferente medida.
- Sus diagonales dividen el rectángulo en dos triángulos rectángulos iguales, permitiendo aplicar el Teorema de Pitágoras para hallar la diagonal, que sería la hipotenusa.
- Por esta característica la fórmula para la diagonal es
. Para el rectángulo de ejemplo sería:
.
- Cada diagonal biseca a la otra, es decir; el punto en donde las diagonales se intersecan, divide a cada una en dos partes iguales.
- El punto donde se cruzan las dos diagonales se llama centro de simetría del rectángulo.
Perímetro y área
Perímetro
El perímetro se calcula sumando la medida de todos los lados del rectángulo, sin embargo; como el rectángulo tiene lados iguales dos a dos el perímetro será el doble de la suma de dos de sus lados diferentes.
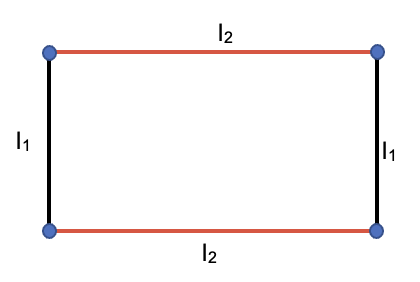
Área
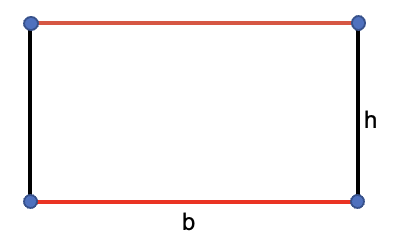
Para hallar el área de un rectángulo, se considera la medida de la base y la altura.
Publicidad, continua debajoSin embargo, como el rectángulo es un paralelogramo con lados paralelos e iguales dos a dos, la base coincide con uno de los lados y la altura corresponde al otro lado de diferente medida.
Por esto se define el área de un rectángulo, como el producto de la medida de sus lados diferentes, es decir; el lado de mayor longitud por el lado de menor longitud.
Ejercicios resueltos
Ejercicio #1
Problema a resolver: ¿Cuál es la diagonal de un rectángulo con una base de 10 mts y una altura de 24 mts?
Ver solución
La fórmula para hallar la diagonal de un rectángulo es
La diagonal mide 26 metros.
Ejercicio #2
Problema a resolver: si un rectángulo cuyos lados desiguales miden 15 metros y 25 metros. Hallar el perímetro y el área del rectángulo.
Ver solución
Por ser un rectángulo el perímetro es igual a:
Sustituyendo los valores:
Para calcular el área, las medidas de sus lados una sería la base y otra la altura, por tanto, el área es:
| Bibliografía: |
|---|
|
Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)
Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.