Contenidos

Inicio / Matemática / Geometría / Triángulo isósceles

Triángulo isósceles

Triángulo que tiene dos lados de igual longitud y los ángulos opuestos a los lados iguales son de igual amplitud cada uno.

Por

Haude Medina

Tabla de contenidos:

Definición

El triángulo isósceles es un tipo de triángulo que tiene dos lados de igual longitud y los ángulos opuestos a los lados iguales son de igual amplitud cada uno.

El triángulo isósceles pertenece a la clasificación de los triángulos según la medida de sus lados.

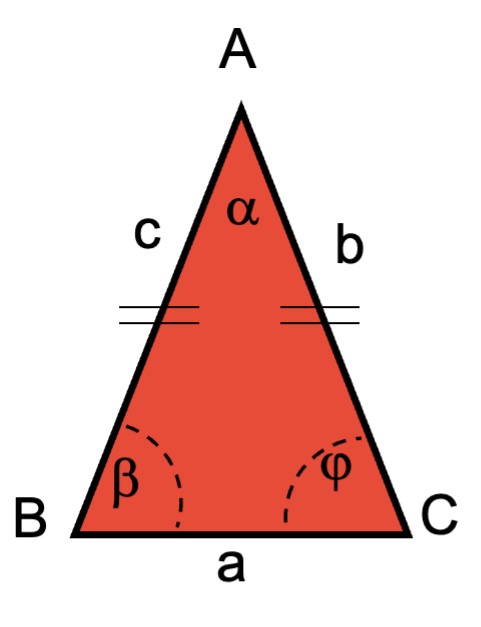
Imagen de un triángulo isósceles.

Los elementos del triángulo isósceles que se muestran en la figura son los siguientes:

Vértices: que se denotan con las letras mayúsculas A, B, C.
Lados: $\overline{AB}$ , $\overline{BC}$ , $\overline{CA}$ , también se pueden identificar con las letras minúsculas a, b, c. Donde los dos lados $\overline{AB}\$ y $\overline{CA}$ son de igual longitud. Entonces, b = c y “a” sería la base del triángulo.
Ángulos interiores: α, β, φ. Los tres suman 180º. Cabe notar que si b = c entonces β = φ.

Características

Los triángulos isósceles presentan características en común, a continuación se presentan estas propiedades:

Se reconocen por tener dos lados iguales y dos ángulos internos iguales, opuestos a los lados congruentes.
El ángulo de diferente amplitud se forma de los lados iguales.
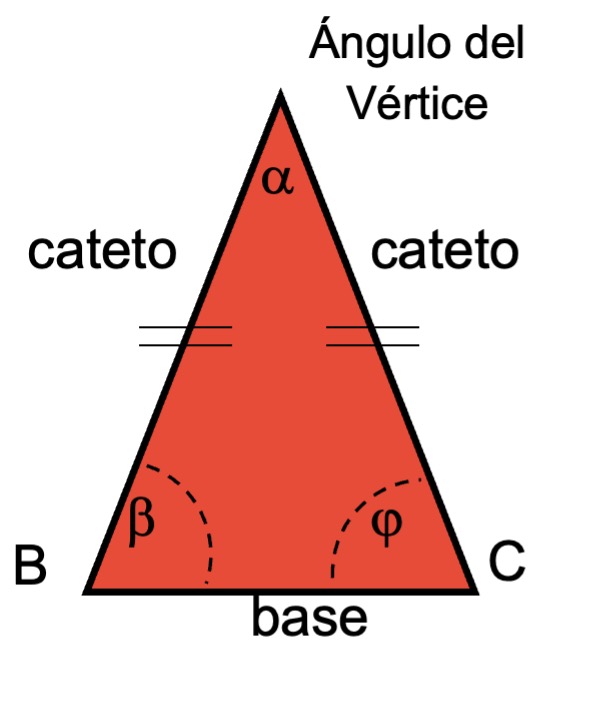
Los dos lados iguales se les denomina como catetos, mientras que el ángulo entre ellos se llama ángulo del vértice.
El lado de longitud diferente es opuesto al ángulo del vértice y se conoce como base del triángulo isósceles.
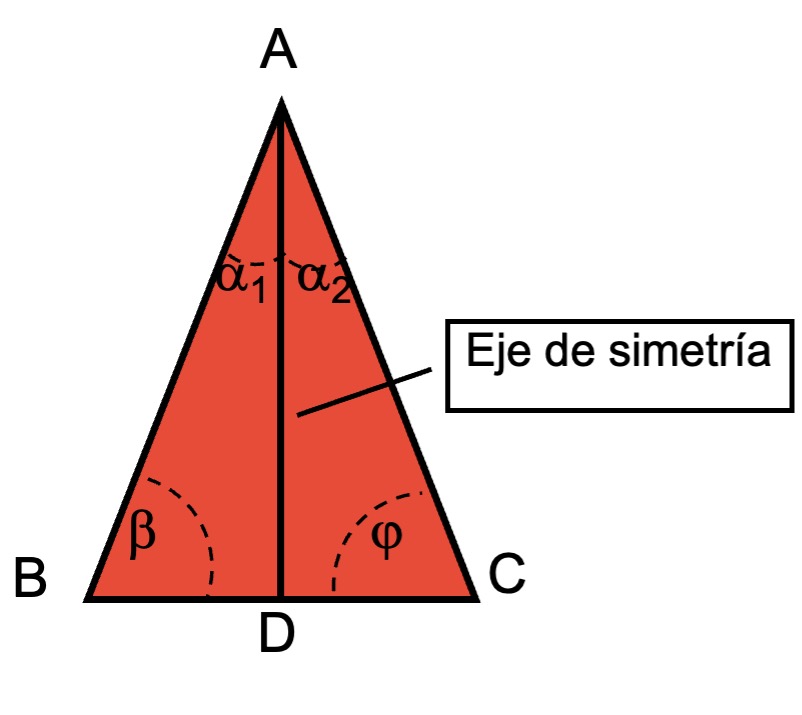
La perpendicular trazada desde el ángulo del vértice divide el triángulo isósceles en dos triángulos congruentes y también se conoce como eje de simetría. De esto se infiere que $\overline{BD}=\ \overline{DC}\$ y los ángulos α₁ y α₂.

Tipos y clasificación

Ya se conoce que los triángulos isósceles provienen de la clasificación de los triángulos según sus lados. No obstante, este tipo de triángulo se puede combinar con la clasificación de los triángulos según sus ángulos, obteniendo los siguientes tipos:

Triángulo rectángulo isósceles: el ángulo desigual mide 90° y los otros dos son iguales a 45°. Es decir, tiene un ángulo recto.
Triángulo obtusángulo isósceles: el ángulo desigual es mayor a 90° (ángulo obtuso) y los otros dos son ángulos agudos.
Triángulo acutángulo isósceles: todos sus ángulos son menores de 90° (ángulos agudos), y los otros dos tienen la misma medida.

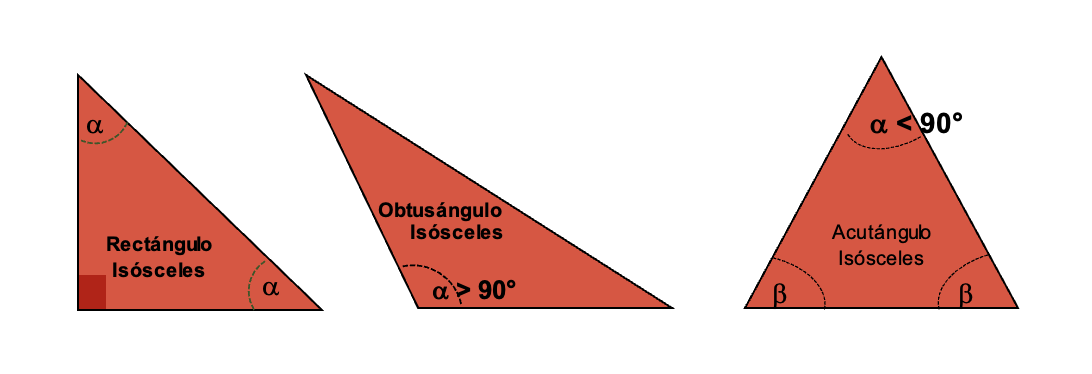
Tipos de triángulos isósceles.

Publicidad, continua debajo

Es de destacar, que la característica de tener dos ángulos internos de igual amplitud se mantiene.

Perímetro y área

Perímetro

El perímetro (P) de un triángulo isósceles se halla sumando la medida de sus tres lados. $P=\ l_1+l_2+l_3$ . Sin embargo, como dos de sus lados son de igual medida, simplificando la fórmula se obtiene:

$P=\ {2l}_1+l_2$

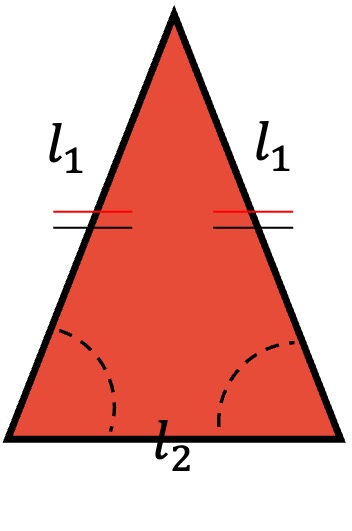
Perímetro de un triángulo isósceles.

Área

El área del triángulo Isósceles (A), se halla multiplicando la base del triángulo por la altura dividido entre dos.

$A=\frac{b\ast h}{2}$

Si se desconoce la altura, esta se calcula mediante el teorema de Pitágoras de donde se deduce la fórmula:

$h=\sqrt{a^2-\frac{b^2}{4}}$

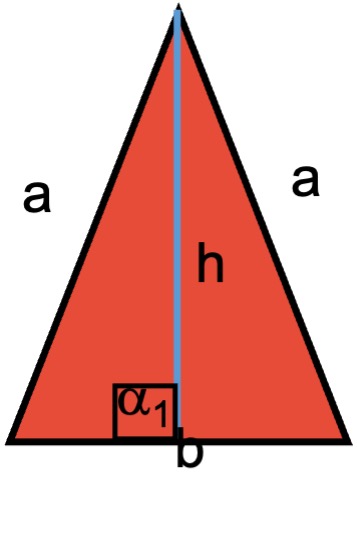
Área del triángulo isósceles.

Sustituyendo esta fórmula en la utilizada para calcular el área del triángulo se obtiene:

$A=\frac{b\ast\sqrt{a^2-\frac{b^2}{4}}}{2}$

Ejercicios resueltos

Ejercicio #1

Problema a resolver: hallar el perímetro de un triángulo isósceles, conociendo que la base mide 48 centímetros y los lados iguales, cada uno mide 72 centímetros.

Ver solución

Para hallar el perímetro se utiliza la fórmula $P=\ {2l}_1+l_2$ .

Donde $l_1$ son los lados iguales y $l_2$ es la base. Sustituyendo los valores en la fórmula:

$P=\left(2\ast72\right)+48=144+48$

$P=192\$ centímetros.

Ejercicio #2

Problema a resolver: para un triángulo isósceles cuya base mide 16 centímetros y un lado lateral mide 10 centímetros. Calcular el área.

Ver solución

Se conoce que la fórmula para encontrar el área de un triángulo isósceles es.

$A=\frac{b\ast\sqrt{a^2-\frac{b^2}{4}}}{2}$

Para el ejemplo $a=10\$ centímetros y $b=16\$ centímetros, sustituyendo estos valores en la fórmula del área se tiene:

$A=\frac{16\ast\sqrt{{10}^2-\frac{{16}^2}{4}}}{2}=\frac{16\sqrt{100-64}}{2}$

$A=\frac{16\sqrt{36}}{2}=\frac{16\ast6}{2}=\frac{98}{2}$

$A=48\$ netímetros².

Bibliografía:
Almaguer, G. (2008). Matemáticas 2. Editorial Limusa. Godino, J. D. y Ruiz, F. (2003). Geometría y su didáctica para maestros. Departamento de Didáctica de las Matemáticas. Universidad de Granada. Matemáticas para 1.er curso de ESO. (2016). Santillana. Ministerio de Educación del Ecuador, (2016). Matemática 8° Grado. Texto del Estudiante. Quito, Ecuador.

¿Te resultó útil este artículo?

¡Genial!

Ayúdanos a mejorar

¡Gracias por tu valoración! Tu contribución nos permite seguir creando contenido que llega gratuitamente a millones de personas por mes:

USD

Acerca del autor:

Haude Medina

Ingeniería Informática (Universidad Rafael Belloso Chacín). Diplomatura en educación universitaria (Universidad José Gregorio Hernández). Magister en gerencia educativa (Universidad Rafael Urdaneta)

Citar este artículo:

Al citar este artículo, reconoces la autoría original, previenes plagios y brindas a tus lectores la posibilidad de acceder a las fuentes originales para obtener más información o verificar datos.

Haude Medina (2022). Triángulo isósceles. Recuperado de Enciclopedia Iberoamericana (https://enciclopediaiberoamericana.com/triangulo-isosceles/). Última edición: mayo 2024. Consultado el 17 de junio de 2024.

Copiar cita

¡Cita copiada a portapapeles!